Env

# install IDE Anaconda Venv
conda env list
conda create --name <venv_name> python==<version>
conda activate <venv_name>
conda list
conda deactivate

# install Nvidia GetForce Driver
nvidia-smi

# install by pip or conda, attention to version alignment
# torch from https://pytorch.org/ based on CUDA_VERSION
# Sci-computer Lib, such as torchsummary, pandas,matplotlib, scikit-learn...
# transformers datasets accelerate

# bak
conda create --name <venv_name>_bak --clone <venv_name>
conda env remove --name <venv_name>_bak

# proxy
vim ~/.bashrc
PROXY_SERVER="http://your_proxy_server_ip:port"
export http_proxy="$PROXY_SERVER"
export HTTP_PROXY="$http_proxy"
export https_proxy="$PROXY_SERVER"
export HTTPS_PROXY="$https_proxy"
# export all_proxy="socks5://your_proxy_server_ip:port"
# export ALL_PROXY="$all_proxy"
# export no_proxy="localhost,127.0.0.1,::1,.local"
# export NO_PROXY="$no_proxy"
export HF_ENDPOINT=https://hf-mirror.com
export HF_XET_CACHE=https://hf-mirror.com/xet
source ~/.bashrc

# verify
# export HUGGINGFACE_TOKEN=<token>
hf auth login
hf auth whoami

Tensor

一种专用于神经网络GPU计算的多维数组结构

  • 各种创建操作torch.[create_function]([**args])：[**args]作用下，以[create_function]方式创建tensor，包括list、arr、numpy、share_memory data、zeros、ones、full、eye、empty、rand、randn、andint、normal、arange、linspace、logspace、zeros_like、ones_like、rand_like等等，注意数据是值传递还是地址传递

  • 各种数学运算[math_function]([**args])：tensor与[**args]进行``[math_function]`的运算，包括sqrt、log、exp、abs、neg、reciprocal、sigmoid、tanh、relu、mask、cat、stack、chunk、expand、einsum等等

  • 基本属性

    • data：tensor不需要梯度计算的复制品

    • dtype：tensor的数据类型

    • device：tensor的存储设备，默认cpu

    • shape / size()：tensor的维度大小

    • ndim / dim()：tensor的维度数量

    • numel()：tensor中元素的总数量

  • 梯度相关

    • requires_grad：tensor是否需要计算梯度，默认False，通过目标函数最终的标量结果backward(retain_graph=true)累加批次所有梯度，默认计算图自动销毁，无法重复求梯度；最后再通过优化器step()更新tensor的data
    • grad：tensor的梯度信息，初始为None，其下zero_()进行梯度清空
    • grad_fn：创建该tensor的函数，用于反向传播
    • is_leaf：tensor是否为叶子节点，用于反向传播

  • 内存布局

    • stride()：tensor各维度在内存中的步长
    • is_contiguous()：tensor在内存中是否连续存储
    • storage()：tensor的底层存储对象
    • storage_offset()：tensor数据在存储中的偏移量

  • 数据类型转换

    • to([type])：将tensor数据转换为指定类型
    • int(), long(), float(), double(), bool()：快捷类型转换方法

  • 设备转换

    • cuda()：转移到GPU设备
    • cpu()：转移到CPU设备
    • to([device])：转移到指定设备

  • 形状转换

    • reshape([shape])：重新调整tensor形状，等价于contiguous + view
    • view([shape])：创建新的tensor视图
    • permute([dims])：重新排列维度
    • transpose([dim0], [dim1])：交换两个维度
    • squeeze()：移除大小为1的维度
    • unsqueeze([dim])：在指定位置增加维度
    • flatten([start_dim], [end_dim])：展平tensor

  • 数据转换

    • numpy()：转换为NumPy数组（需在CPU）
    • tolist()：转换为Python列表
    • item()：提取标量值
    • detach()：分离计算图，返回不需要梯度的tensor
    • clone()：创建tensor的深拷贝
    • contiguous()：返回内存连续的tensor

  • 广播机制：从右向左（低维到高维）对齐维度，通过自动补1扩展维度，并最终将大小为1的维度复制扩展，以使两个张量具有运算兼容的形状

  • nn.Parameter([tensor])：张量参数化，存于model.parameters()，框架要求其中的tensors都具有梯度更新，才可再由优化器统一更新

NN

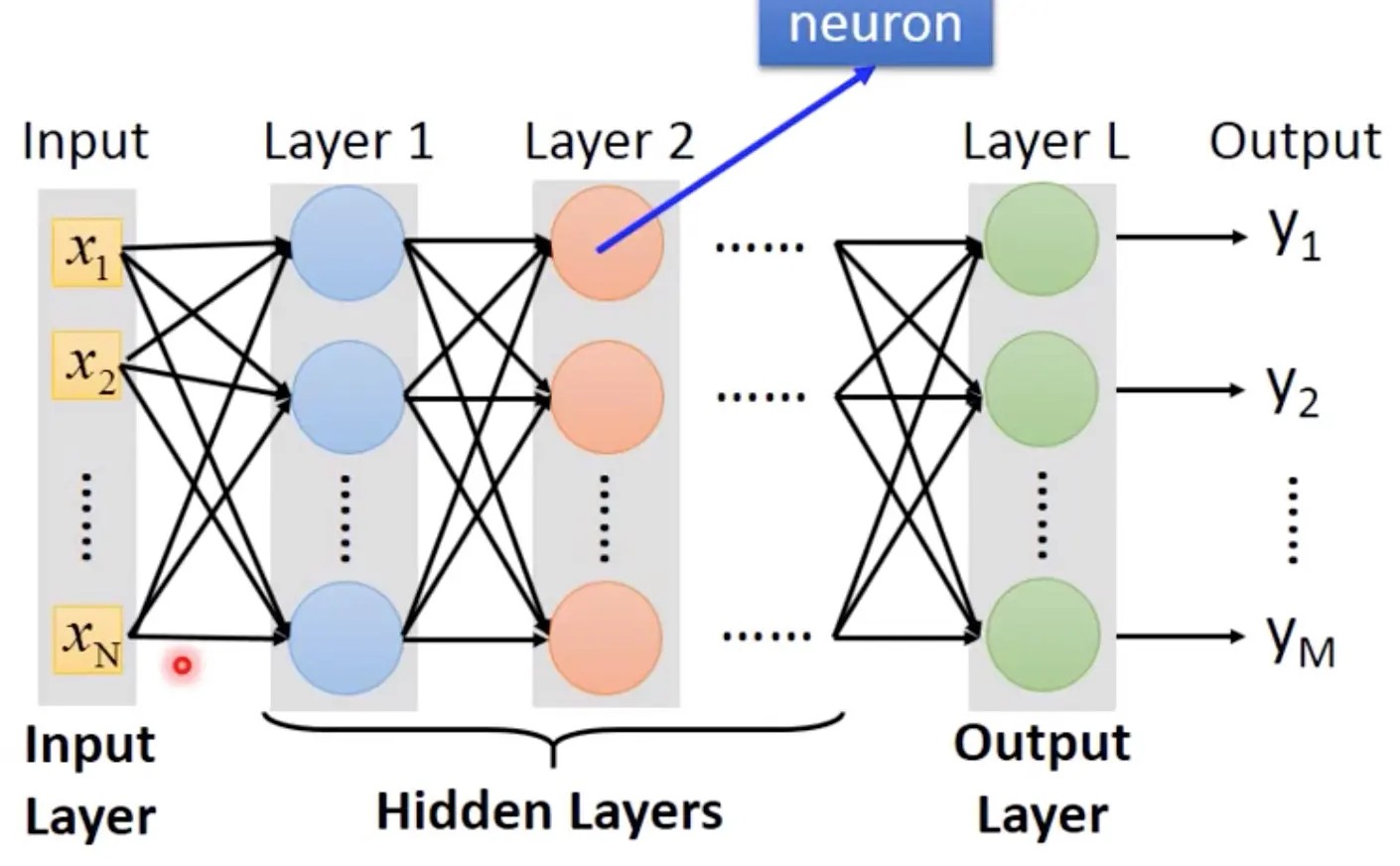
$$ \textbf{y} = model(\textbf{x}) \quad model = h_L \circ h_{L-1} \circ \cdots \circ h_1 $$
  • 神经元（Neuron）：计算基本单元，形式化表示为 $h_{\textbf{w,b}}(\textbf{x})=f(\textbf{w}^T \textbf{x} + \textbf{b})$ ，堆叠学习输入数据的层次化特征表示
    • 权重（$\textbf{w}^T$）：控制每个输入特征对神经元输出的影响程度
    • 偏置（$\textbf{b}$）：调节激活函数的触发阈值
    • 激活函数（$f$）：影响反向传播的梯度流动，控制神经元的激活与抑制
  • 层（Layers）：经过神经元组合结构后产生的数据，一般神经网络结构依次为输入层（Input Layer）负责接收原始数据 $\rightarrow$ 隐藏层（Hidden Layers）进行特征提取 $\rightarrow$ 输出层（Output Layer）根据目标归纳为最终预测
  • 模型（Model）：任务的规律函数

网络训练过程：首先输入数据通过模型前向传播（Forward Propagation）得到预测输出；随后利用损失函数（Loss Function）计算预测值与真实值之间的误差，并通过链式法则（Chain Rule）推导出各参数关于损失函数的梯度；接着模型反向传播（Back Propagation），基于梯度下降法，利用合适的优化器（Optimizer），在一定学习率（Learning Rate）下更新参数$\Delta \textbf{w}$和$\Delta \textbf{b}$，从而优化模型；通过多次迭代，模型逐步调优权重和偏置，最终使前向传播后损失函数计算的误差达到较小，获得性能较优的模型用于实践。

Activation Function

为避免多层神经网络退化为单层结构，同时帮助深度网络能够有效处理高维复杂任务，需要在每个神经元后引入非线性激活函数：

函数名表达式图像区间单调性对称性可微性导数
Sigmoid$\sigma(x) = \frac{1}{1 + e^{-x}}$
$\sigma'(x) = \sigma(x) \cdot (1 - \sigma(x))$		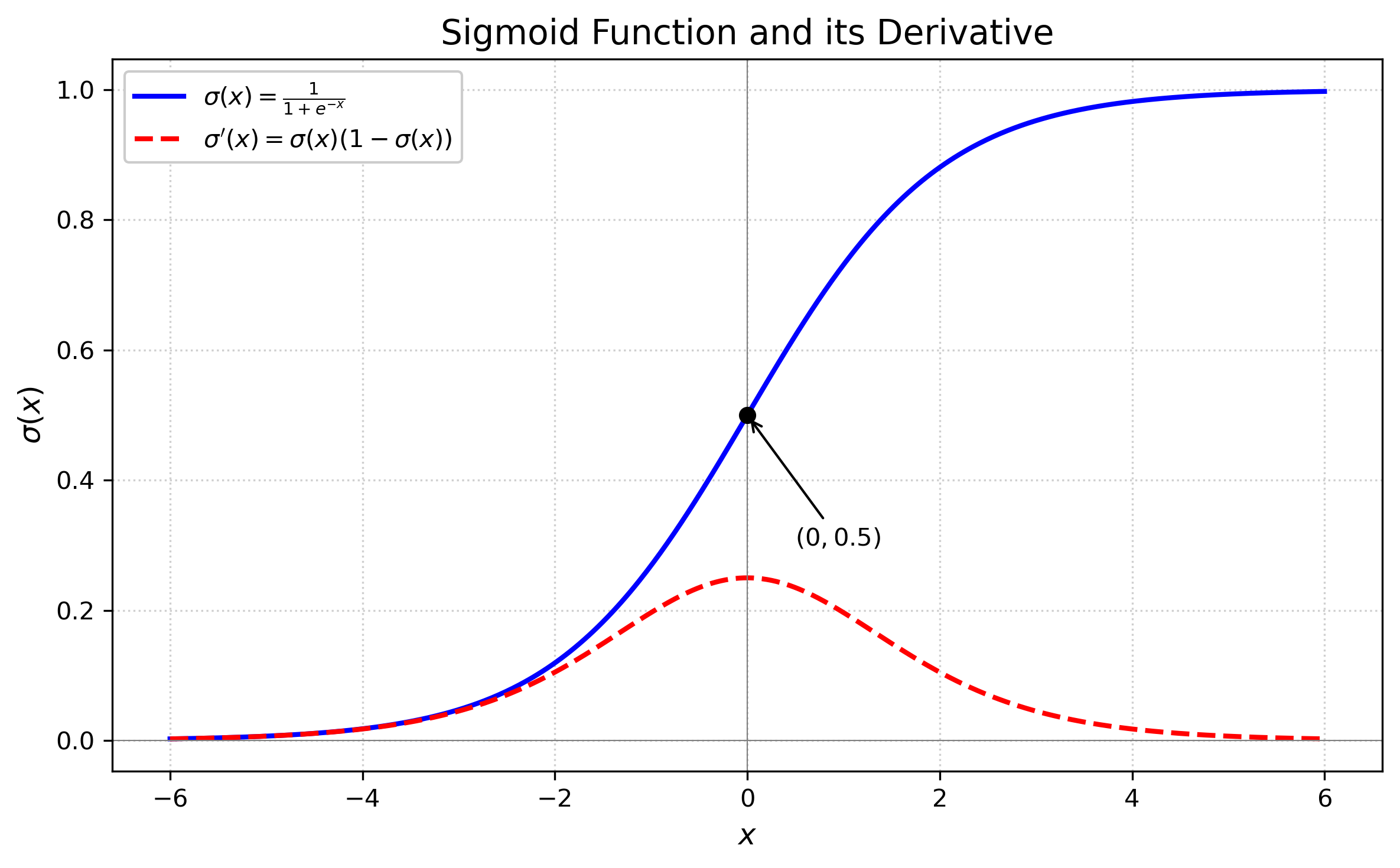sigmoid(0,1)，适合将实数映射到概率单调递增关于原点不对称光滑（连续可导）计算高效，但当输入值很大或很小时，梯度消失，训练耗时
Tanh$\tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}$
$\tanh'(x) = 1 - \tanh^2(x)$		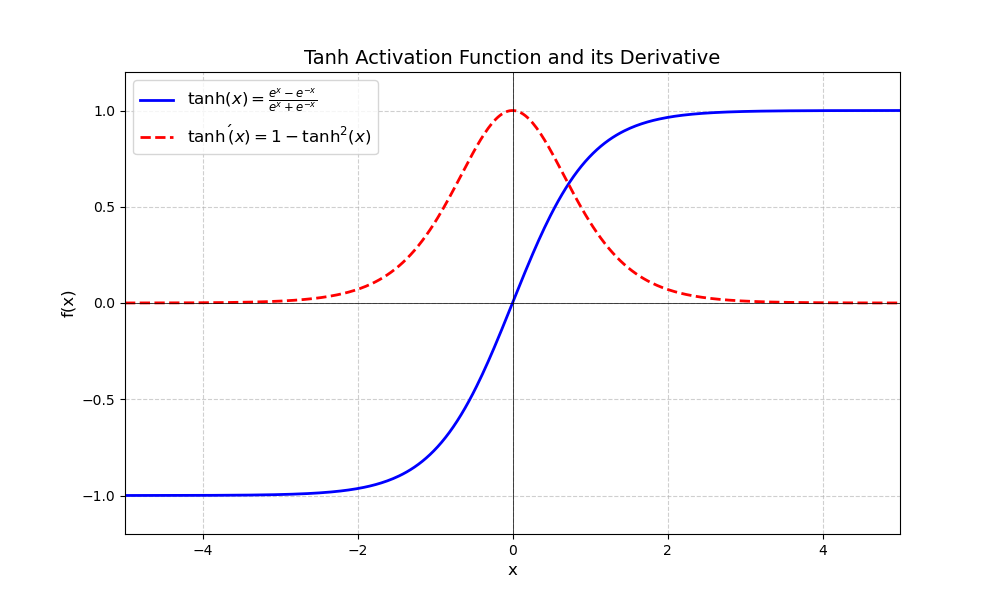tanh(-1,1)，适合于数据归一化单调递增关于原点对称，具有正负一致性光滑（连续可导）计算高效，值大方便模型收敛，但当输入值很大或很小时，梯度消失，训练耗时
ReLU$\text{ReLU}(x) = \begin{cases} x & \text{if } x > 0 \\ 0 & \text{if } x \leq 0 \end{cases}$
$\text{ReLU}'(x) = \begin{cases} 1 & \text{if } x > 0 \\ 0 & \text{if } x \leq 0 \end{cases}$		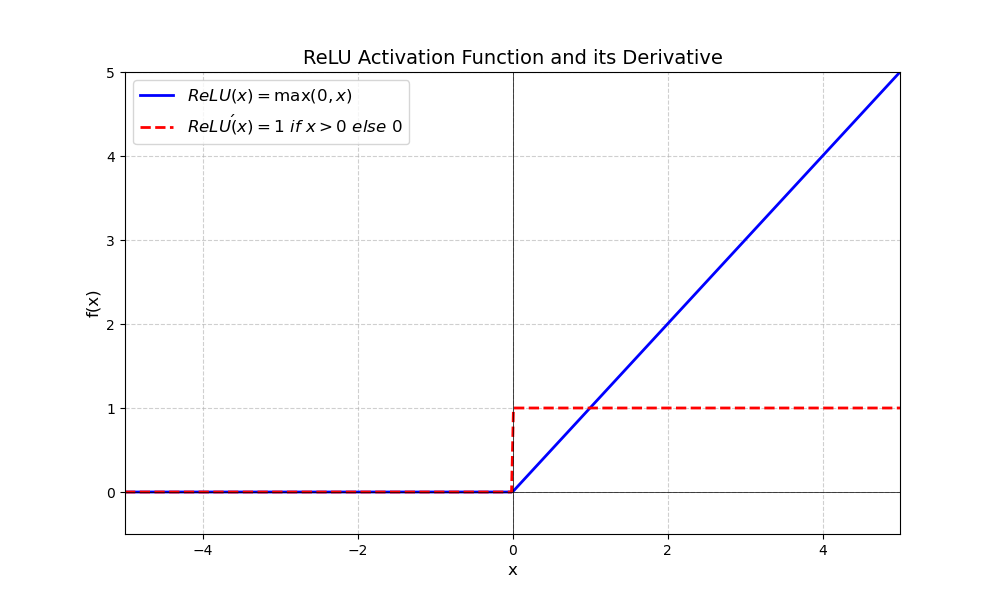relu(0, +∞)，适合于加速网络训练单调不递减关于原点不对称分段，连续可导计算高效，值大方便模型收敛，但可能存在神经元死亡
Leaky ReLU$f(x) = \begin{cases} x & \text{if } x \geq 0 \\ \alpha x & \text{if } x < 0 \end{cases}$
$f'(x) = \begin{cases} 1 & \text{if } x \geq 0 \\ \alpha & \text{if } x < 0 \end{cases}$		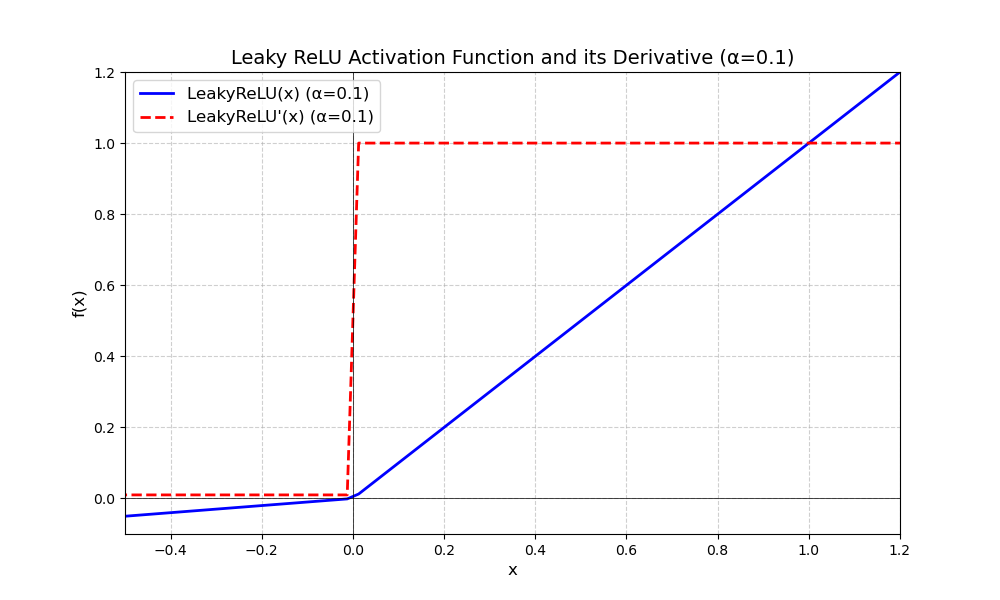leakyRelu(-∞, +∞)，适合于解决梯度消失单调递增关于原点不对称分段，连续可导计算高效，值大方便模型收敛，但超参不好确定

Loss Function

衡量预测值与真实值的差异，Pytorch中作为层可自定义：

函数名表达式解释优点缺点
Mean Squared Error$J(x) = \frac{1}{2n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$考虑事件独立，计算实际模型与理想模型的差距梯度稳定，训练高效；适合大规模严格回归任务；平方项使得模型对离群点敏感，鲁棒性较差；
Cross Entropy$H(\hat{y}_i,y_i) = - \frac{1}{n} \sum_{i=1}^{n} y_i \log \hat{y}_i$考虑事件独立，最大似然估计实际模型作为理想模型的概率与softmax结合，适合大规模严格分类任务；包括softmax单标签|sigmoid多标签分类要求分类类别互斥；梯度不稳定，需谨慎处理低置信度的错误样本；

Optimizer

通过损失函数应用链式法则对所有参数计算偏导数（即梯度），随后以预设的学习率$\alpha$沿梯度下降方向更新参数，使得下次迭代时损失函数计算的误差降低：

$$ \textbf{w}_{new} = \textbf{w}_{old} - \alpha \frac{\partial J(w)}{\partial w} \quad \textbf{b}_{new} = \textbf{b}_{old} - \alpha \frac{\partial J(b)}{\partial b} $$

优化过程常见的问题包括：

  • $\alpha$过小时模型收敛过慢，$\alpha$过大时模型收敛振荡
  • 鞍点梯度停滞问题
  • 局部极小值问题
优化器特点优点适用情况
MBGD以小批次（batch）数据的平均梯度更新防止振荡不独立使用
Momentum当前梯度动量 = 动量系数 X 历史累计梯度动量 + （1 - 动量系数） X 当前小批次梯度跳出局部最优图像分类任务，卷积神经网络
Adagrad当前学习率 = 标准学习率 / 历史累计梯度平方均值学习率关于差值自适应稀疏数据任务、NLP 早期模型
RMSprop当前学习率 = 标准学习率 / 根号下，（自适应系数 X 历史累计梯度平方和 + （1 - 自适应系数） X 当前小批次梯度平方）可调自适应时序数据处理任务，循环神经网络
Adam融合Momentum动量和RMSprop学习率方法，并使用 $\frac{1}{1-参数^t}$纠正累计梯度动量和累计梯度平方和纠正几乎所有深度学习任务
AdamW在Adam基础上，当前梯度 = Adam梯度 - 衰减系数 X 当前小批次梯度权重衰减BERT、GPT 等 Transformer 模型

FCNN/MLP

FCNN $$ L_i(n_i) -> L_j(n_j): \quad \begin{align*} \mathbf{W}_{ij} | \mathbf{b}_j = \begin{bmatrix} w_{11} & w_{12} & \cdots & w_{1n_i} \\ w_{21} & w_{22} & \cdots & w_{2n_i} \\ \vdots & \vdots & \ddots & \vdots \\ w_{n_j1} & w_{n_j2} & \cdots & w_{n_j n_i} \end{bmatrix} \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_{n_j} \end{bmatrix} \end{align*} $$
  • 全连接（Full Connect）：相邻层所有神经元之间均相互连接，同一层神经元之间无连接

优点：易于实现，可拟合任意连续函数；擅长学习输入数据的全局模式；

缺点：参数量大，计算成本高；局部模式（如图像空间）捕捉能力弱，需手动设计特征；

CNN

simpleCNN

cnn $$ OH = \frac{H + 2P - FH}{S} + 1 \quad OW = \frac{W + 2P - FW}{S} + 1 $$
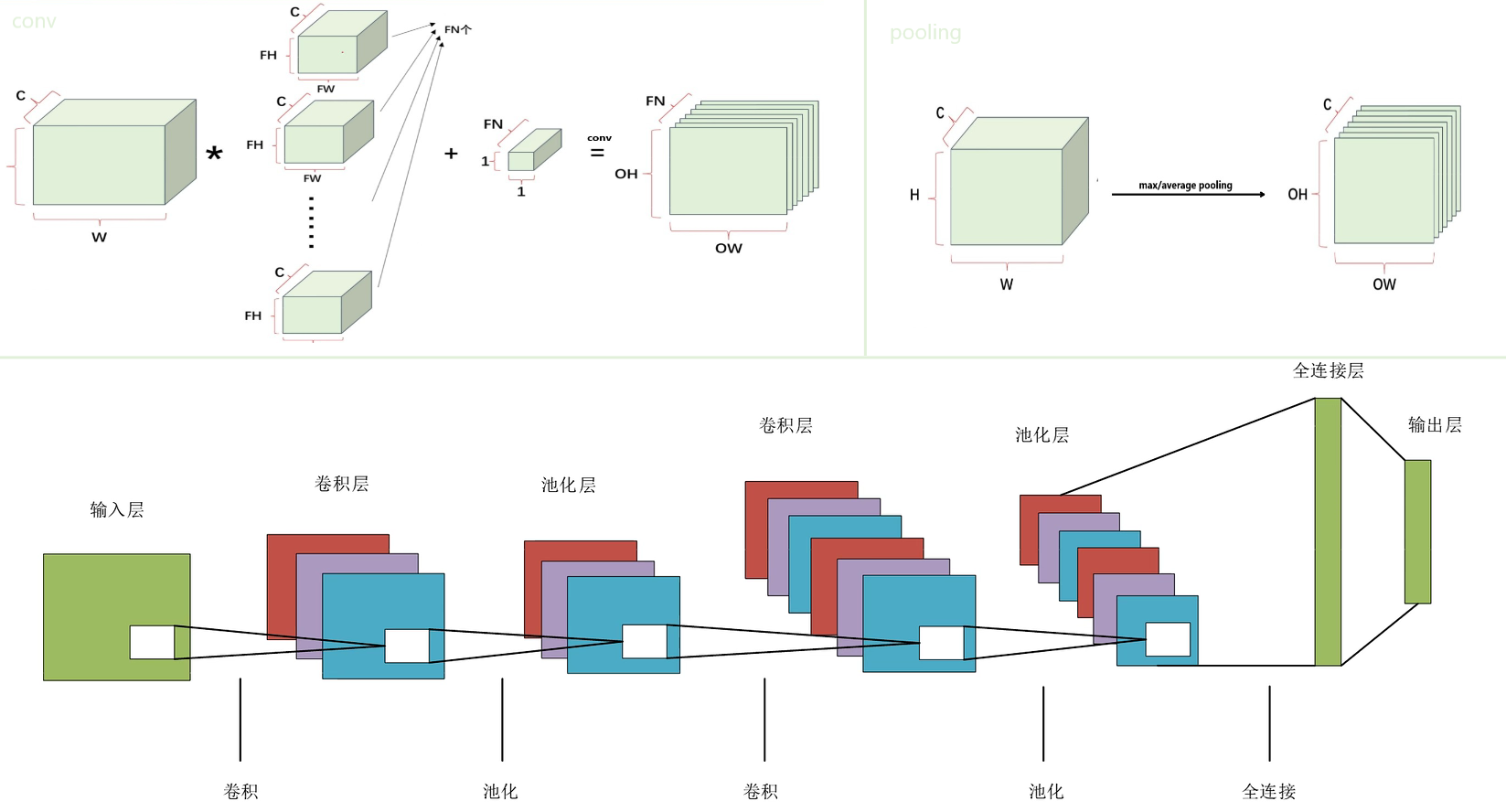
  • 特征提取（Feature Extraction）：
    • 卷积（Convolutions）：考虑步幅、填充，提取原数据中与卷积核特征相同的区域，产生通道数和特征图大小的变化
    • 池化（Pooling）/ 下采样（Subsampling）：考虑步幅、填充，按感受野数据降维，减弱对输入小幅平移的敏感程度，产生特征图大小的变化
    • 参数共享（Param Share）：同一卷积核在输入不同位置滑动并复用参数，计算效率高

优点：适合处理网格状数据；

缺点：输入矩阵大小固定；需要大量标注数据；解释性较弱；

LeNet-5

lenet-5
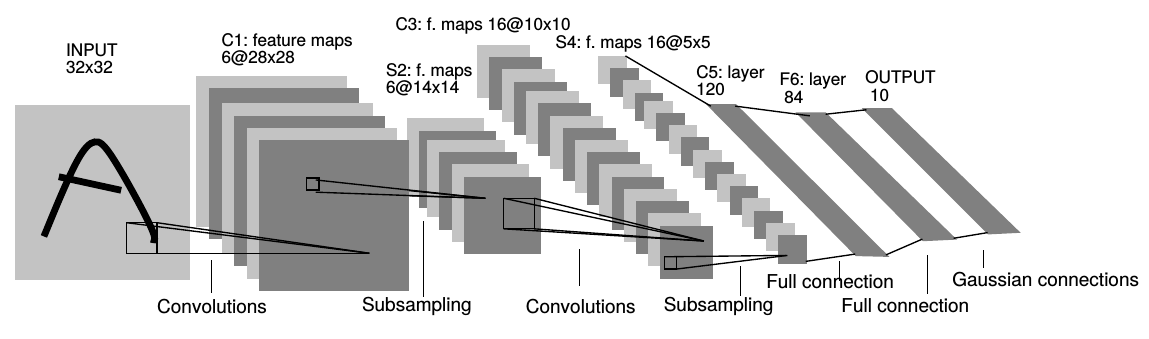
层类型（5）参数设置输出尺寸
Input32×32×1（原始 MNIST 输入大小）32×32 灰度图像
Conv1（Sigmoid/Tanh）6 个 5×5 卷积核，步长 1，填充 028×28×6
Subsampling1（Average）2×2 平均池化，步长 2，填充 014×14×6
Conv2（Sigmoid/Tanh）16 个 5×5 卷积核，步长 1，填充 010×10×16
Subsampling2（Average）2×2 平均池化，步长 2，填充 05×5×16
FC3（ReLU、Flatten）120 个神经元120×1
FC4（ReLU）84 个神经元84×1
Output（Softmax）10 个神经元10×1（对应 0-9 数字分类）
  • 经典层级结构：N *（卷积 + 池化）+ 全连接
  • 平均池化（Max Pooling）：数据降维的同时，尽可能还原数据特征

优点：大幅减少参数量，计算效率高；

缺点：网络层数浅，只适合小数据集；平均池化会模糊特征；sigmoid激活容易导致梯度消失，训练不稳定；全连接层占大部分参数，易过拟合；

AlexNet

alexnet
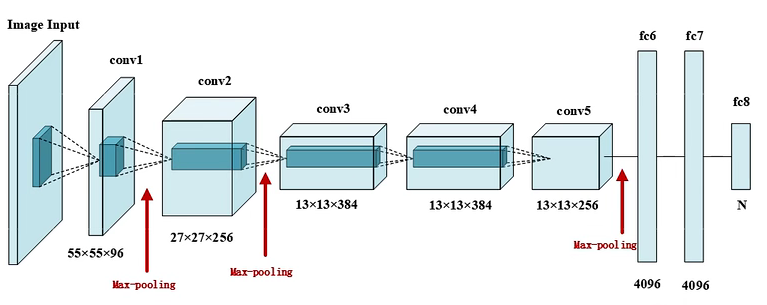
层类型（8）参数设置输出尺寸
Input224×224×3（ImageNet输入大小）227×227×3 RGB图像（双GPU并行）
Conv1（ReLU）96 个 11×11×3 卷积核，步长 4，填充 055×55×96
Pooling1（Max）3×3 池化，步长 2，填充 027×27×96
Conv2（ReLU）256 个 5×5×96 卷积核，步长 1，填充 227×27×256
Pooling2（Max）3×3 池化，步长 2，填充 013×13×256
Conv3（ReLU）384 个 3×3×256 卷积核，步长 1，填充 113×13×384
Conv4（ReLU）384 个 3×3×384 卷积核，步长 1，填充 113×13×384
Conv5（ReLU）256 个 3×3×384 卷积核，步长 1，填充 113×13×256
Pooling5（Max）3×3 池化，步长 2，填充 06×6×256
FC6（ReLU、Flatten、Dropout）4096 个神经元4096
FC7（ReLU、Dropout）4096 个神经元4096
FC8（Softmax）1000 个神经元1000（对应 ImageNet 1000 类分类）

  • 数据增强（Data Augmentation）：通过翻转、裁剪、PCA等操作，提高数据量，同时防止过拟合

  • 随机失活（Dropout）：一种正则化方法，每轮迭代时，随机去除层间部分神经元的连接，关闭前向传播和反向传播，防止过拟合

  • 局部响应归一化（LRN）：按通道对每个位置进行归一化，增强局部对比度，但其实作用不大

    $$ b_{x,y}^i = \frac{a_{x,y}^i}{\left( k + \alpha \sum_{j=\max(0, i-n/2)}^{\min(N-1, i+n/2)} (a_{x,y}^j)^2 \right)^\beta} $$

  • ReLU激活：梯度稳定，收敛加快

  • 最大池化（Max Pooling）： 保留显著特征

优点：网络层数更深，适合更大数据集；

缺点： 参数量大，计算成本高；大卷积核效率低；

VGG-16

vgg
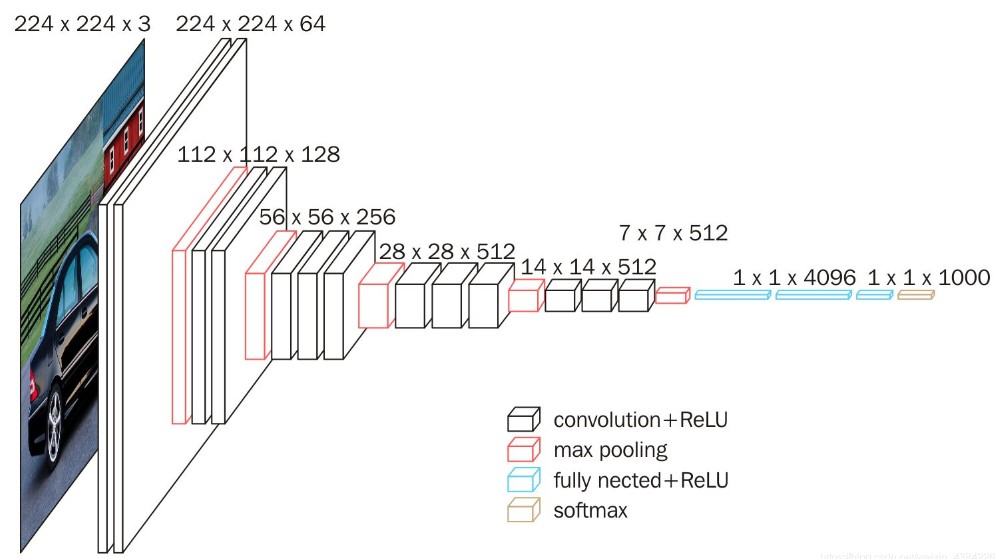
层类型（16）参数配置输出尺寸
Input224×224×3（ImageNet输入大小）224×224×3 RGB图像
Conv1_1（ReLU）64 个 3×3 卷积核，步长 1，填充 1224×224×64
Conv1_2（ReLU）64 个 3×3 卷积核，步长 1，填充 1224×224×64
Pooling1（Max）2×2 池化，步长 2，填充 0112×112×64
Conv2_1（ReLU）128 个 3×3 卷积核，步长 1，填充 1112×112×128
Conv2_2（ReLU）128 个 3×3 卷积核，步长 1，填充 1112×112×128
Pooling2（Max）2×2 池化，步长 2，填充 056×56×128
Conv3_1（ReLU）256 个 3×3 卷积核，步长 1，填充 156×56×256
Conv3_2（ReLU）256 个 3×3 卷积核，步长 1，填充 156×56×256
Conv3_3（ReLU）256 个 3×3 卷积核，步长 1，填充 156×56×256
Pooling3（Max）2×2 池化，步长 2，填充 028×28×256
Conv4_1（ReLU）512 个 3×3 卷积核，步长 1，填充 128×28×512
Conv4_2（ReLU）512 个 3×3 卷积核，步长 1，填充 128×28×512
Conv4_3（ReLU）512 个 3×3 卷积核，步长 1，填充 128×28×512
Pooling4（Max）2×2 池化，步长 2，填充 014×14×512
Conv5_1（ReLU）512 个 3×3 卷积核，步长 1，填充 114×14×512
Conv5_2（ReLU）512 个 3×3 卷积核，步长 1，填充 114×14×512
Conv5_3（ReLU）512 个 3×3 卷积核，步长 1，填充 114×14×512
Pooling5（Max）2×2 池化，步长 2，填充 07×7×512
FC6（ReLU、Flatten、Dropout）4096 个神经元4096
FC7（ReLU、Dropout）4096 个神经元4096
FC8（Softmax）1000 个神经元1000（对应 ImageNet 1000 类分类）
  • 块状（Block）简洁结构：带填充卷积保持分辨率，最大池化减半，可移植性强
  • 小卷积核：参数少，训练效果和大卷积核差不多

优点：参数多，理解力强；

缺点：参数多，算力要求高；网络深，易梯度消失或梯度爆炸，依赖权重初始化；

GoogLeNet

googlenet
层类型（22）参数配置输出尺寸
Input224×224×3（ImageNet输入大小）224×224×3 RGB图像
Conv1（ReLU）64 个7×7 卷积核，步长 2，填充 3112×112×64
Pooling1（Max）3×3 池化，步长 2，填充 156×56×64
Conv2（ReLU）64 个1×1 卷积核，步长 1，填充 056×56×64
Conv3（ReLU）192 个3×3 卷积核，步长 1，填充 156×56×192
Pooling3（Max）3×3 池化，步长 2，填充 028×28×192
Inception 4a~4b2 个 Inception 模块28×28×480
Pooling4（Max）3×3 池化，步长 2，填充 014×14×480
Inception 5a~5e5 个 Inception 模块14×14×832
Pooling5（Max）3×3 池化，步长 2，填充 07×7×832
Inception 6a~6b2 个 Inception 模块7×7×1024
Pooling6（ALL Average）7×7 全局平均池化1×1×1024
FC（Flatten、Softmax、Dropout）1000 个神经元1000（对应 ImageNet 1000 类分类）
  • Inception 模块：
    • 多尺度特征融合：并行应用不同尺寸的卷积核和池化，要求不同路径输出保持高宽不变，在通道维度（超参）上连接，捕捉不同感受野的特征，特征提取能力强
    • 1×1 卷积降维：实现上一层特征图跨通道的交互和信息整合，减少通道数，降低计算量
    • 并行分支：“宽而浅”的设计，实现高精度低计算量
  • 全局平均池化（GAP）：输出只和通道数相关，替代全连接层，大幅减少参数量，抑制过拟合但易信息丢失
  • 辅助分类器（auxiliary classifiers）：在中间层添加辅助 Softmax 输出，增强梯度回传，缓解深层网络梯度消失问题，避免过拟合，效果有限

优点：计算高效，参数量少；

缺点：结构复杂，调试困难；对小数据集易过拟合；

ResNet-18

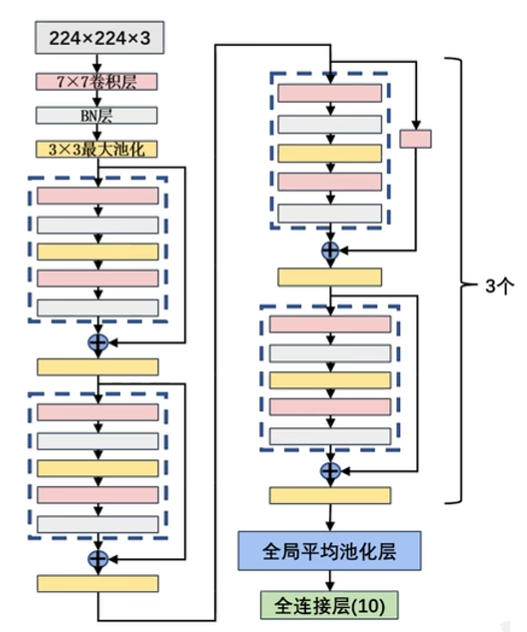
resnet8
层类型（18）参数配置输出尺寸
Input224×224×3（ImageNet输入大小）224×224×3 RGB图像
Conv1（ReLU、BN）64 个 7×7卷积核，步长2，填充 3112×112×64
Pooling1（Max）3×3最大池化，步长2，填充 156×56×64
Stage12 个残差块（每个块含 2 个 3×3 卷积，直连跳跃连接）56×56×64
Stage22 个残差块（每个块含 2 个 3×3 卷积，前一个下采样跳跃连接）28×28×128
Stage32 个残差块（每个块含 2 个 3×3 卷积，前一个下采样跳跃连接）14×14×256
Stage42 个残差块（每个块含 2 个 3×3 卷积，前一个下采样跳跃连接）7×7×512
Pooling5（ALL Average）全局平均池化1×1×512
FC（Flatten、Softmax、Dropout）1000 个神经元1000（对应 ImageNet 1000 类分类）

  • 残差（Stage）：

    • 跳跃连接（Skip Connection）：提供直连或 1x1 卷积，要求不同路径输出各维度保持一致，缓解【深度网络-梯度消失/爆炸】无法保持恒等状态而模型退化的问题，允许网络选择性地学习残差$F(X) - x$，至少不会比浅层网络更差
    $$ F(x) = H(x) + h(x) $$
    • 批量标准层（Batch Normalize）：$ \gamma, \beta$持续训练，对多批次特征图任一维度调整（统一量纲、移动数据分布区间到激活函数高梯度范围），加快模型收敛速度，使模型更稳定 $$ y_i = \gamma \cdot \left( \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} \right) + \beta \\ \mu_B = \frac{1}{m}\sum_{i=1}^m x_i \quad \sigma_B^2 = \frac{1}{m}\sum_{i=1}^m (x_i - \mu_B)^2 \quad \epsilon > 0 \quad \gamma, \beta $$

优点：为深度学习打下基础；迁移学习，作为预训练模型效果好；

缺点：跳跃连接可能引入噪声；

DenseNet-121

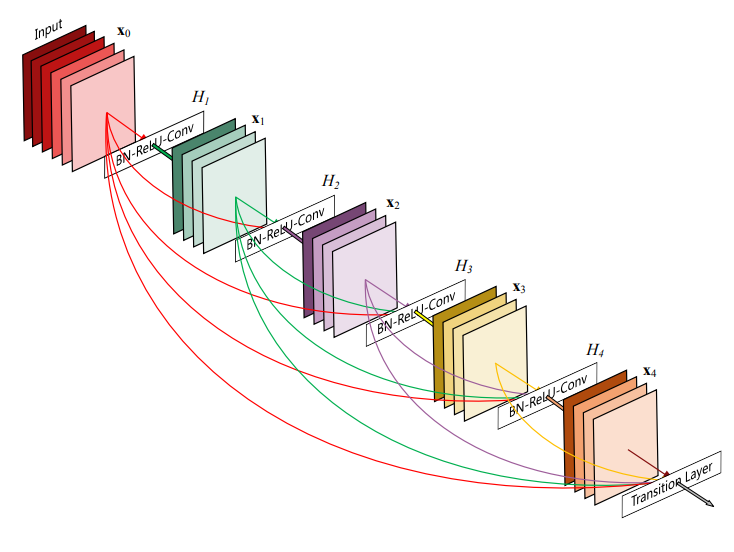
densenet
层类型（121）参数配置输出尺寸
Input224×224×3（ImageNet输入大小）224×224×3 RGB图像
Conv1（ReLU、BN）64 个 7×7卷积核，步长2，填充 3112×112×64
Pooling1（Max）3×3最大池化，步长2，填充 156×56×64
Dense16 层密集块（growth rate =32）56×56×256
Trans1128 个 1×1 卷积核 → 2×2 平均池化28×28×128
Dense212 层密集块（growth rate =32）28×28×512
Trans2256个 1×1 卷积核 → 2×2 平均池化14×14×256
Dense324 层密集块（growth rate =32）14×14×1024
Trans3512个 1×1 卷积核 → 2×2 平均池化7×7×512
Dense416 层密集块（growth rate =32）7×7×1024
Pooling5（ALL Average）全局平均池化1×1×1024
FC（Flatten、Softmax、Dropout）1000 个神经元1000（对应 ImageNet 1000 类分类）

  • 密集连接（Dense Connection）：每一单元的输入来自前面所有单元的输出，显著提升特征复用能力和计算效率

    • 增长率（Growth Rate）：特征提取单元输出特征图的通道数
    • 瓶颈系数（Bottleneck Factor）：特征提取单元中间层输出特征图的通道数，平衡计算效率和特征表达能力

  • 过渡层（Transition Layer）：控制模型复杂度，使用平均池化对局部区域取平均值，能保留整体特征的分布

优点：特征复用性强；参数高效；缓解梯度消失；正则化效果以防止过拟合；

缺点：计算复杂，内存消耗高；

RNN

simpleRNN

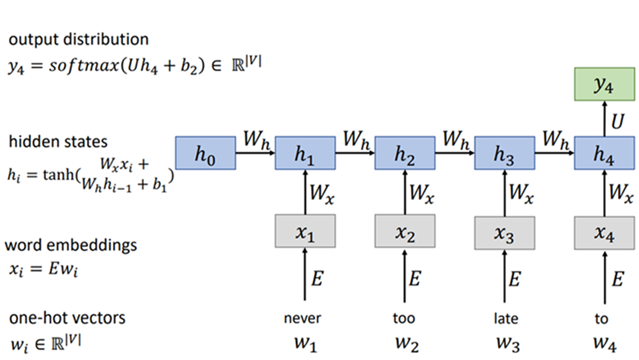
simpleRNN

  • 循环连接（时间步）：允许序列信息在各个时间步之间传递，每个时间步的输出取决于当前时刻的输入和上一时刻的隐藏状态，这种隐藏状态包含了上文信息

  • 参数共享（Param Share）：泛化到不同长度的样本，提高计算效率，防止过拟合

  • 隐藏连接（隐藏层）

优点：适合处理序列数据；

缺点：序列计算方式，训练较慢；时间步信息太长，容易产生梯度消失/爆炸；

LSTM

LSTM
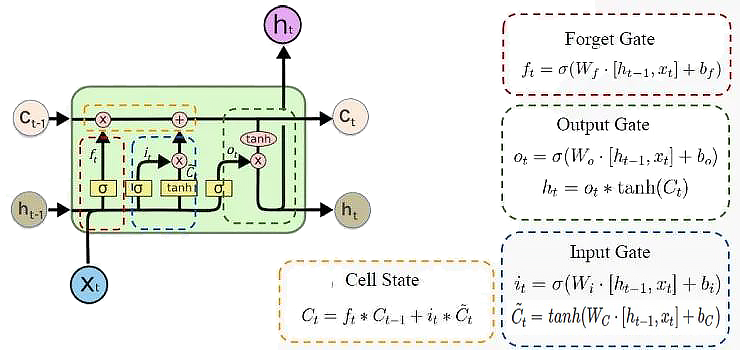
  • ”记忆细胞“状态（$C_{t-1} \rightarrow C_t$）：保存历史时刻中的有效信息
  • 权重门控结构：选择性记忆或遗忘信息
    • 遗忘门（Forget Gate）：淡化过去时间步信息
    • 输入门（Input Gate）：淡化当前时间步信息
    • 输出门（Output Gate）：激活当前及其之前时间步信息，同时解决梯度问题

优点：缓解梯度消失/爆炸；

缺点：无法捕捉长期依赖关系；并行化困难；计算复杂度高，内存消耗大，可能过拟合；

GRU

GRU
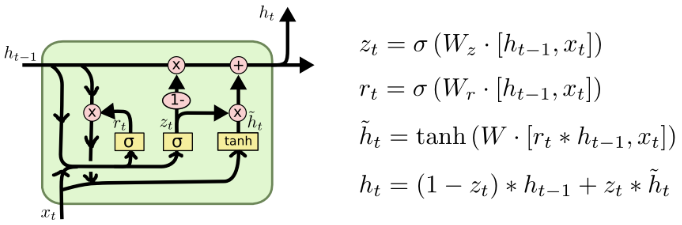
  • 权重门控结构：选择性更新或重置信息
    • 重置门$r_t$（Reset Gate）：淡化过去时间步信息
    • 更新门$z_t$（Update Gate）：平衡过去和当前时间步信息的权重

优点：缓解梯度问题，降低结构复杂性，训练效率高；

缺点：无法捕捉长期依赖关系；并行化困难；

Transformer

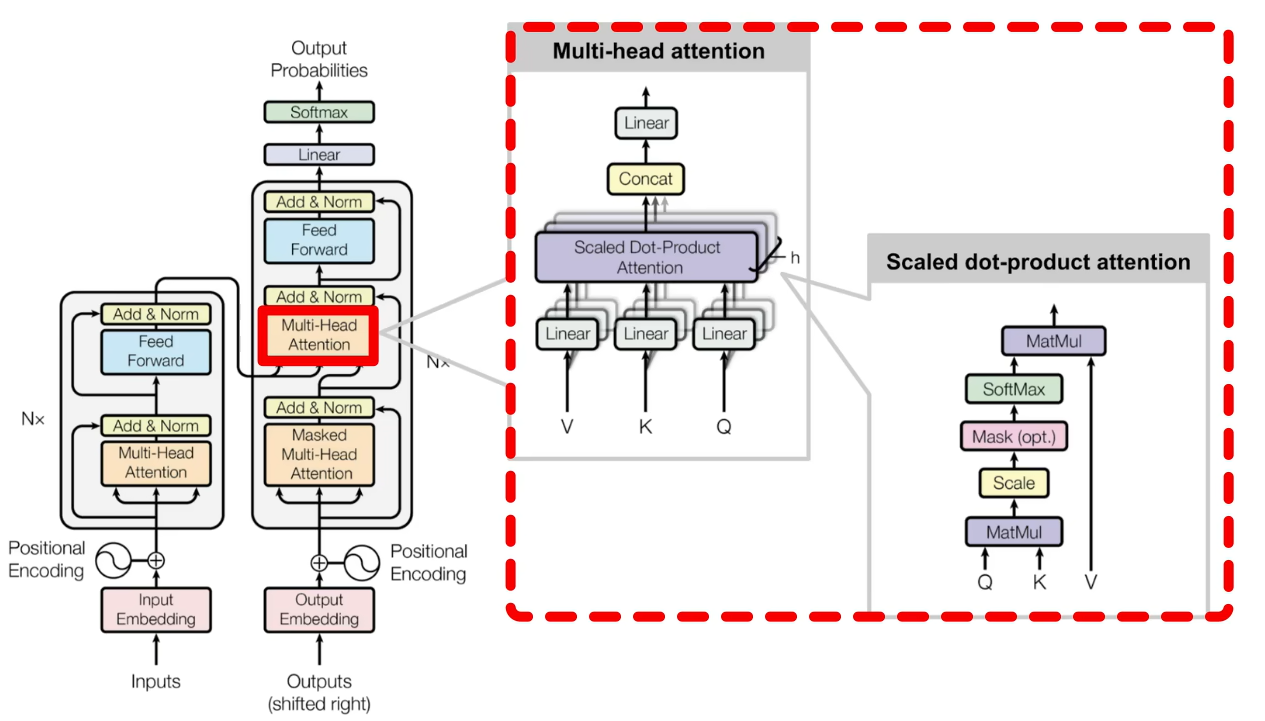
transformers

仅依赖自注意力机制（Self-Attention） 来处理序列数据，这使得模型能够：

  1. 并行计算：序列中各位置同时处理，训练速度快
  2. 捕捉长距离依赖：注意力机制直接建模任意两个位置之间的关系
  3. 可解释性：注意力权重可视化，展示 token 间的依赖关系
  4. 训练效率高：充分利用 GPU 的并行计算能力

Transformer 采用编码器-解码器（Encoder-Decoder） 结构：

编码器: 输入序列 → [编码器层 × N] → 编码器输出
解码器: 编码器输出 + 目标序列 → [解码器层 × N] → 输出概率分布

首先，自然语言经过 tokenizer 划分为词元（token），不同词元对应一个索引，接着，经过 Transformer 变形，核心组件包括：

  • 词嵌入（Input Embedding）：依赖训练好的词嵌入矩阵查表，将输入 token 映射为固定维度的稠密向量

    所谓词嵌入矩阵本质上是对 token 的 onehot 编码进行数据降维，降低模型计算复杂度。

    同时使得语义相近 token 向量靠近，语义差异 token 向量分散，便于之后在向量空间中做点积相似度计算，表达词与词之间的特征关系。

  • 位置编码（Positional Encoding）：向词向量中加入时序信息，让模型区别词在句子中的顺序，从而实现并行计算

    $$ PE_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) \\ PE_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) \\ $$

    每个词向量、每个维度都有独特的编码。

    任意位置 $ pos+k $ 的编码可以表示为位置 $ pos $ 的编码的线性函数，让模型能够学习到词与词之间的相对位置关系，更好地进行长序列泛化。

  • 自注意力机制

    • 缩放点积注意力（Scaled Dot-Product Attention）：编码器使用，考虑每个词与句子中所有其他词语的关系，从而更准确地理解这个词在当下语境中的含义

      每个输入 token 会生成三个向量，查询（Query, Q）–> 当前 token 想要关注什么，键（Key, K）–> 当前 token 能提供什么信息，值（Value, V）–> 当前 token 的实际信息内容。

      利用三个线性变换矩阵 $\text{W}_q、\text{W}_k、\text{W}_v$ 将每个词向量映射为 $\text{Querys}, \text{Keys}, \text{Values}$ 向量，再以缩放点积的方式计算不同词向量之间 $\text{Querys}$-$\text{Keys}$ 相似度矩阵，每个词向量依据其与其他词向量的相似度，求对应值向量 $\text{Values}$ 加权和，作为该词向量具有上下文信息注意力分配的新词向量表示。

    $$ \mathbf{Q} = \mathbf{X}\mathbf{W}_q, \mathbf{K} = \mathbf{X}\mathbf{W}_k, \mathbf{V} = \mathbf{X}\mathbf{W}_v \

    \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)V $$

    • 多头注意力（Multi-Head Attention）：将输入 token 经过不同的 Q、K、V 线性投影到不同的子空间并行计算注意力，然后拼接结果

      不同“头”学习到不同的语言模式，比如有的头关注语法关系，有的头关注语义相似性，有的头关注代词指代等，将不同头输出拼接起来，维度不发生变化，从而捕获输入序列中不同类型的依赖关系，增强模型的表征能力。

    • 掩码注意力（Causal Attention）：解码器使用，在预测第 t 个位置的输出时，禁止模型“看到”第 t 个位置之后（未来）的信息。

      在计算不同词向量之间 $\text{Querys}$-$\text{Keys}$ 相似度矩阵后，使用一个上三角矩阵，让当前行之后的列的权重为 -inf，再经softmax 会把对应位置的注意力权重变成 0，从而生成具有上文信息注意力分配的新词向量表示。

    • 交叉注意力（Cross Attention）：连接编码器和解码器，Query 来自解码器，而 Key 和 Value 则来自编码器输出

      解码器在生成每个词时，发出Q请求，关注到输入序列的所有K，V 信息

  • 残差连接：将子层的输入直接加到输出上，缓解该子层带来的梯度消失

  • 层归一化：在特征维度上进行归一化，调整数据分布，加快模型收敛，同时使使模型更稳定

  • 前馈神经网络（Feed-Forward Network, FFN）：每个位置的 token 独立经过相同的两层全连接网络，先升维再降维

    注意力机制主要负责在不同位置之间进行信息交流和聚合。

    前馈网络则对每个位置独立地进行更复杂的特征变换和非线性映射，增强模型的表达能力。

  • 输出层：解码器输出通过线性变换和 softmax，将向量映射为词汇表大小的概率分布，预测下一个 token。

  • Teacher Forcing 训练：一次性将完整的目标序列（但经过了适当的掩码）输入解码器，并行地预测每个位置的输出（下一位置 token 的预测），此时只需要将目标序列向左移动一个位置，与预测输出做多元分类交叉熵损失。

  • Auto Regressive 推理：解码器逐个生成 logits，解码出 token 并加入输入序列中，预测下一个 token（初始 token 为起始符，末尾 token 为终止符），直到预测出终止符；解码时，基于 temperature、top-p、top-k、贪心、Beam Search 采样。

RoPE

LN

  • Post LN
  • Pre LN
  • RMSNorm

activation

  • ReLU
  • GeLU
  • SwiGLU
  • GeGLU

strcture

  • Encoder - Decoder
  • Encoder only
  • Dncoder only
  • Casual Encoder
  • Casual Decoder
  • Prefix Decoder

architecture

MoE

混合专家模型，为由多个单独网络（“专家”）组成的系统建立一个监管机制，每个“专家”处理训练样本的不同子集，专注于输入空间的特定区域；设置门控网络|路由分配每个“专家”的权重或决定哪些Token被发送到哪些“专家”；在训练过程中，这些专家和门控网络都同时接受训练，以优化它们的性能和决策能力。

  • 组件专家：允许将 MoE 嵌入到多层网络中的某一层，如 Transformer 的 FFN

  • 条件计算：基于输入Token动态激活或停用网络组件

  • 负载均衡：门控算法抑制Token不均匀分配和“专家”训练不均匀

    • 专家容量：Token处理阈值，”专家“都达到处理上限后，Token通过残差溢出到下一层
    • 稀疏稳定性：容量因子、dropout
    • 专业程度：编码器“专家”各司其职；解码器“专家”较低专业化程度。

  • 并行计算：MoE 层在不同设备间共享，而其他所有层则在每个设备上复制

  • 万亿参数：极高模型规模，节省计算资源，高效预训练，高速推理

  • 微调策略：稀疏部分正则化；负载均衡算法；MoE层冻结；较小批次大小和较大学习率

  • 缺点：显存消耗高；（稀疏部分）易过拟合，泛化能力不足，微调困难；不适合重理解任务

  • 优点：适合知识密集型任务；从指令微调中获益；多任务学习

moes
  • 共享专家（Shared Expert）：所有 tokens 都会经过的共享专家，每个 token 会用计算的 Router 权重，来选择 topK 个专家，然后和共享的专家的输出一起加权求和；捕捉通用、全局的特征信息，减少不同专家间的知识冗余，提升计算效率

Q->KV