Basic
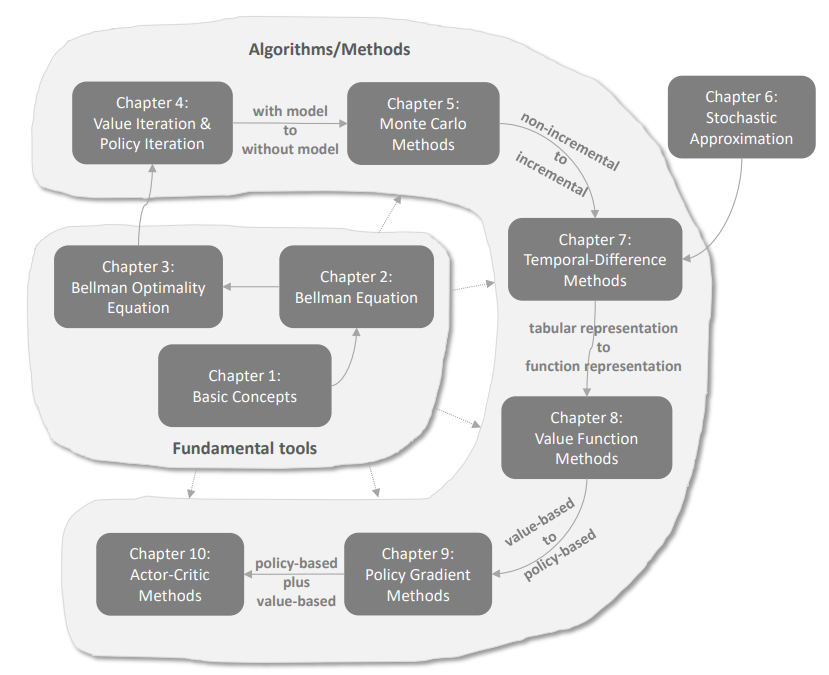
Concepts
与监督学习对比,强化学习利用环境带来的奖励自收敛,无需大量标注数据,通过试错学习最优策略:
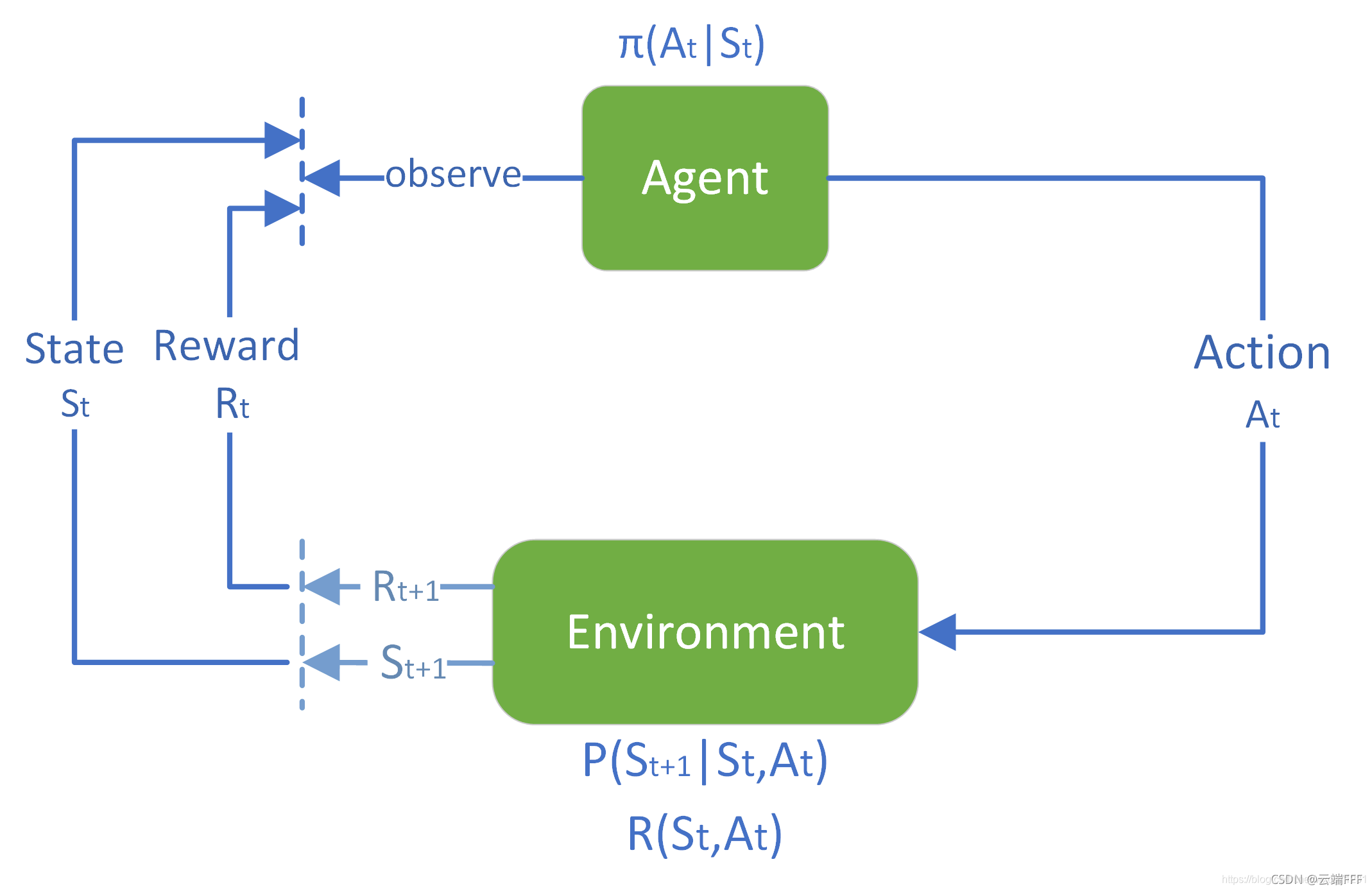
State:状态($s$),环境在特定时刻的描述,代表了智能体所处的情况
迷宫游戏中指当前智能体在迷宫中的位置
状态可以是完全可见的(完全可观测环境),也可以是部分可见的(部分可观测环境)
Action:动作($a_j(s_i)$),智能体在某个状态下执行的操作,动作和环境会导致智能体状态发生改变
- 迷宫游戏中指当前智能体在当前位置 向上/向下/向左/向右 移动一格
- 动作空间可以是离散的(如向上下左右移动),也可以是连续的(如方向盘转动角度)
Policy:策略($\pi(a_{ij}|s_i)$),智能体的决策核心,它规定了在任意状态应该采取什么动作
- 迷宫游戏中指当前智能体的操作决策,可通过表格或者条件概率分布(神经网络)描述
- 直接决定了智能体的行为,强化学习的最终目标就是找到一个最优策略,以最大化长期回报
State transition:状态转移($p(s_k|s_i,a_j)$),环境的“物理法则”,描述了环境和动作对状态的作用
- 迷宫游戏中指当前智能体在当前位置移动一格的下一个格,可通过表格或者条件概率分布描述
- 定义了环境的不确定性和规则,智能体无法直接改变状态转移,只能通过选择不同的动作来间接影响状态转移的结果
Reward:奖励($p(r_k|s_i,a_j)$),环境在智能体执行一个动作后,反馈给智能体的一个影响
- 迷宫游戏中指当前智能体在当前位置移动一格到下一个格带来的标量信号,可通过表格或者条件概率分布(神经网络)描述
- 定义了强化学习问题的目标,一种即时反馈,告诉智能体某个动作在某个状态下是好是坏
- 0 没有惩罚,一般看作为奖励信号
Trajectory:轨迹($τ = (s₀, a₀, r₁, s₁, a₁, r₂, s₂, a₂, r₃, ..., s_T)$),智能体在一段时间内,与环境进行完整一次交互的全过程记录,包含了从起始状态到终止状态的一系列状态、动作和奖励
- Return:累积奖励,最大化其长期获得的总奖励,而不是眼前的即时奖励,更能衡量一个状态或一个轨迹的长期价值
- Episode:有限轨迹,从初始状态开始,到终止状态结束的一次完整交互过程,与之相对的是 Continuing,持续轨迹
智能体(Agent)在环境(Environment)的某个状态(State)下,根据策略(Policy)选择一个动作(Action),环境随之状态转移(State transition),并给予智能体一个奖励(Reward)。智能体通过不断重复这个过程,以学习最大化其回报(Return)的最优策略。MDP 表示为:
集合 (Sets)
- 状态空间 (State space):所有状态的集合,记为 $\mathcal{S}$
- 动作空间 (Action space):与每个状态 $s \in \mathcal{S}$ 相关联的动作集合,记为 $\mathcal{A}(s)$
- 奖励集合 (Reward set):与每个状态-动作对 $(s,a)$ 相关联的奖励集合,记为 $\mathcal{R}(s,a)$
模型 (Model)
- 状态转移概率 (State transition probability):在状态 $s$ 下采取动作 $a$,转移到状态 $s'$ 的概率为:$p(s'|s,a)$,满足对于任意 $(s,a)$:$\sum_{s' \in \mathcal{S}} p(s'|s,a) = 1$
- 奖励概率 (Reward probability):在状态 $s$ 下采取动作 $a$,获得奖励 $r$ 的概率为:$p(r|s,a)$,满足对于任意 $(s,a)$:$\sum_{r \in \mathcal{R}(s,a)} p(r|s,a) = 1$
策略 (Policy):在状态 $s$ 下选择动作 $a$ 的概率为:$\pi(a|s)$,满足对于任意 $s \in \mathcal{S}$:$\sum_{a \in \mathcal{A}(s)} \pi(a|s) = 1$
马尔可夫性质 (Markov Property):随机过程的无记忆特性,下一个状态或奖励仅取决于当前状态和动作,与之前的历史状态和动作无关
$$ p(s_{t+1}|s_t,a_t,s_{t-1},a_{t-1},\ldots,s_0,a_0) = p(s_{t+1}|s_t,a_t) \\ p(r_{t+1}|s_t,a_t,s_{t-1},a_{t-1},\ldots,s_0,a_0) = p(r_{t+1}|s_t,a_t) $$
Bellman Equation
基于折扣因子(Discounted rate)($\gamma \in [0,1]$)的理想累计未来折扣奖励:
$$ G_t=R_{t+1}+{\gamma}R_{t+2}+{\gamma }^2R_{t+3}+... $$递归推导可以发现,当前状态的理想累计未来奖励依赖于其他状态的:
$$ G_t=R_{t+1} + \gamma G_{t+1} $$状态价值($V^{\pi}(s)$),指从某个状态 $s$ 开始出发,经过一致的 $\pi$,所能获得的 Return:
$$ V^{\pi}(s) = \mathbb{E}_\pi[G_t∣S_t = s]=\mathbb{E}_\pi[R_{t+1}∣S_t = s] + \gamma \mathbb{E}_\pi[G_{t+1}∣S_t = s] $$第一部分 $\mathbb{E}_\pi[R_{t+1}∣S_t = s]$ 是从状态 $s$ 出发能获得的期望立即奖励
$$ \mathbb{E}_\pi[R_{t+1}∣S_t = s] = \sum_{a \in A} \pi(a|s) \cdot r(s,a) = \sum_{a \in A} \pi(a|s) \sum_{r} p(r|s,a) \cdot r $$第二部分 $\gamma \mathbb{E}_\pi[G_{t+1}∣S_t = s]$ 是 从状态 $s$ 出发下一个状态的期望折扣奖励
$$ \mathbb{E}_\pi[G_{t+1}∣S_t = s] = \sum_{a \in A} \pi(a|s) \sum_{s' \in S}p(s'|s,a) \cdot V^{\pi}(s') $$
综上,得到贝尔曼递归方程 –> 当前状态价值等于所有动作加权平均下立即奖励和未来折扣奖励:
$$ V^{\pi}(s) = \sum_{a \in A} \pi(a|s) \left[ \sum_{r} p(r|s,a) \cdot r + \gamma \cdot \sum_{s' \in S}p(s'|s,a) \cdot V^{\pi}(s') \right] $$向量化整理后,得到,可求解任一状态价值:
$$ \mathbf{v}_\pi = \mathbf{r}_\pi + \gamma \mathbf{P}_\pi \mathbf{v}_\pi \rightarrow \mathbf{v}_\pi = (I - \gamma \mathbf{P}_\pi)^{-1}\mathbf{r}_\pi\\ \text{s.t. } \mathbf{P}_\pi(s,s')= \sum_{a} \pi(a|s) p(s'|s,a) = p(s'|s) $$动作价值($Q^{\pi}(s,a)$),指从某个状态 $s$ 开始出发并选择某个动作 $a$,经过一致的 $\pi$,所能获得的 Return
$$ Q^{\pi}(s,a) = \mathbb{E}_\pi[G_t∣S_t = s, A_t = a] = \sum_{r} p(r|s,a) \cdot r + \gamma \cdot \sum_{s' \in S}p(s'|s,a) \cdot V^{\pi}(s') = \sum_{r} p(r|s,a) \cdot r + \gamma \cdot \sum_{s' \in S}p(s'|s,a) \cdot \sum_{a' \in A}\pi(a'|s')Q^\pi(s',a') $$状态价值是在不同动作价值的加权平均:
$$ V^{\pi}(s) = \mathbb{E}_\pi[G_t∣S_t = s] = \sum_a \pi(a|s) \mathbb{E}_\pi[G_t∣S_t = s, A_t = a] = \sum_a \pi(a|s) Q^{\pi}(s,a) $$
==状态价值定义一个策略及其好坏== -> $\pi_1$ 优于 $\pi_2$:
$$ > V^{\pi_1}(s) \geq V^{\pi_2}(s) \text{ for all s} \in S > $$最优策略 -> $\pi_*$ 优于任一 $\pi$:
$$ > V^{\pi_*}(s) \geq V^{\pi}(s) \text{ for all s} \in S > $$策略最优化:对各个状态,==选择动作价值最大的那个策略==
$$ > \mathbf{v}_\pi =\underset{\pi}{max} (\mathbf{r}_\pi + \gamma \mathbf{P}_\pi \mathbf{v}_\pi)= \underset{\pi}{max}(\sum_a \pi(a|s) Q^{\pi}(s,a)) \text{ for all s} \in S > $$
固定$\mathbf{r}_\pi$、$\gamma$ 和系统$\mathbf{P}_\pi$,随机初始化$\mathbf{v}_\pi$,求新策略 $\pi^{*}$ 使得状态价值最大,即要求使最大化最大动作价值的权重,即 $\pi^*$为选择动作价值最大的那个(在一个关联系统中,你无法孤立地优化某一个状态的价值,正因为存在这种“牵一发而动全身”的依赖关系,我们不能简单地、独立地为每个状态选择当前看起来最好的动作。这直接引申出了不同的优化算法来解决这个挑战)
$$ \text{For any s} \in S: \pi^*(a|s) = \begin{cases} 1 & \text{If } a = \arg\max_{a' \in A} Q^*(s, a') \\ 0 & \text{Else} \end{cases} $$根据收缩映射原理、不动点原理等,贝尔曼公式存在 唯一 不动点 策略 解 $\mathbf{v}_{\pi^*}$,可通过值迭代贪心求出,且$\mathbf{v}_{\pi^*} \geq \mathbf{v}_\pi$,即最优策略的状态价值最大
注意最优策略是针对某一个状态的,可推广到所有状态,决定因素包括:
- $\mathbf{r}_\pi$:系统模型的奖励函数,关键因素,具有线性相对不变性
- $\gamma$ :折损因子,折损未来奖励或惩罚,折损程度和时间步成次方正相关,与因子大小成次方反相关
- 折损因子小,看重短期 Return(奖励或惩罚)
- 折损因子大,看重长期 Return(奖励或惩罚)
- $\mathbf{P}_\pi$:系统模型的状态转移,一般由环境定义,不被人机交互操纵
Algorithm
==价值估计 + 策略优化==
Model-Based
$$ \mathbf{v}_{\pi^{*}} = f(\mathbf{v}_{\pi^{*}}) = \underset{\pi}{max} (\mathbf{r}_\pi + \gamma \mathbf{P}_\pi \mathbf{v}_\pi) $$在非直接计算的前提下,求成立的 $\pi^{*}$ | $\mathbf{v}_{\pi^{*}}$
"""
Args:
S: list or array of states
A: list or array of actions
P: transition probability matrix P[s][a][s'] = p(s'|s,a)
r: reward function r(s,a) or r(s,a,s')
gamma: discount factor (default 0.95)
theta: convergence threshold (default 1e-6)
Returns:
V: optimal value function
policy: optimal policy
"""
# Initialize value function
n_states = len(S)
n_actions = len(A)
# Algorithms
# ...
Value interation
- 策略优化:基于给定 $\mathbf{v}_\pi$,计算$\mathbf{q}_\pi$,最大项对应优化的策略 $\pi^{'} = \arg\max_{\pi} ( \pi(a|s) Q^{\pi}(s,a))$
- 价值更新:基于更新 $\pi^{'}$,计算优化的状态价值 $\mathbf{v}_{\pi^{'}}$
- 迭代步骤1,2直到状态价值稳定
V = np.zeros(n_states)
while True:
delta = 0
# Create temporary value function for synchronous update
V_new = np.zeros(n_states)
for s in range(n_states):
# Calculate Q-values for all actions
Q = np.zeros(n_actions)
for a in range(n_actions):
reward = r(s, a)
future_value = 0
for s_next in range(n_states):
future_value += P[s][a][s_next] * V[s_next]
Q[a] = reward + gamma * future_value
# Update value with maximum Q-value
V_new[s] = np.max(Q)
delta = max(delta, abs(V_new[s] - V[s]))
# Check convergence
V = V_new.copy()
if delta < theta:
break
# Extract optimal policy
policy = np.zeros(n_states, dtype=int)
for s in range(n_states):
Q = np.zeros(n_actions)
for a in range(n_actions):
reward = r(s, a)
future_value = 0
for s_next in range(n_states):
future_value += P[s][a][s_next] * V[s_next]
Q[a] = reward + gamma * future_value
policy[s] = np.argmax(Q)
return V, policy
Policy interation
- 策略评估:基于给定 $\pi$,通过值迭代而非线性方程组,预估$\mathbf{v}_{\pi} = f(\mathbf{v}_{\pi})$
- 策略优化:基于预估 $\mathbf{v}_\pi$,计算$\mathbf{q}_\pi$,最大项对应优化的策略 $\pi^{'} = \arg\max_{\pi} ( \pi(a|s) Q^{\pi}(s,a))$
- 迭代1,2直到策略稳定
policy = np.random.choice(n_actions, size=n_states)
while True:
# Policy Evaluation
V = np.zeros(n_states)
while True:
delta = 0
V_new = np.zeros(n_states)
for s in range(n_states):
a = policy[s]
reward = r(s, a)
future_value = 0
for s_next in range(n_states):
future_value += P[s][a][s_next] * V[s_next]
V_new[s] = reward + gamma * future_value
delta = max(delta, abs(V_new[s] - V[s]))
V = V_new.copy()
if delta < theta:
break
# Policy Improvement
policy_stable = True
for s in range(n_states):
old_action = policy[s]
# Calculate Q-values for all actions
Q = np.zeros(n_actions)
for a in range(n_actions):
reward = r(s, a)
future_value = 0
for s_next in range(n_states):
future_value += P[s][a][s_next] * V[s_next]
Q[a] = reward + gamma * future_value
best_action = np.argmax(Q)
policy[s] = best_action
if old_action != best_action:
policy_stable = False
if policy_stable:
break
return V, policy
Truncated Policy interation
| Policy: | Value iteration | Policy iteration | Comments |
|---|---|---|---|
| 1) Policy: | N/A | $\pi_0$ | |
| 2) Value: | $v_0 = v_{\pi_0}$ | $v_{\pi_0} = r_{\pi_0} + \gamma P_{\pi_0} v_{\pi_0}$ | |
| 3) Policy: | $\pi_1 = \arg\max_{\pi}(r_{\pi} + \gamma P_{\pi} v_0)$ | $\pi_1 = \arg\max_{\pi}(r_{\pi} + \gamma P_{\pi} v_{\pi_0})$ | The two policies are the same |
| 4) Value: | $v_1 = r_{\pi_1} + \gamma P_{\pi_1} v_0$ | $v_{\pi_1} = r_{\pi_1} + \gamma P_{\pi_1} v_{\pi_1}$ | $v_{\pi_1} \geq v_1$ since $v_{\pi_1} \geq v_{\pi_0}$ |
| 5) Policy: | $\pi_2' = \arg\max_{\pi}(r_{\pi} + \gamma P_{\pi} v_1)$ | $\pi_2 = \arg\max_{\pi}(r_{\pi} + \gamma P_{\pi} v_{\pi_1})$ | iter from nested to single |
| : | : | : | : |
max_eval_iters = 5
policy = np.random.choice(n_actions, size=n_states)
while True:
# Truncated Policy Evaluation
V = np.zeros(n_states)
for _ in range(max_eval_iters):
delta = 0
V_new = np.zeros(n_states)
for s in range(n_states):
a = policy[s]
reward = r(s, a)
future_value = 0
for s_next in range(n_states):
future_value += P[s][a][s_next] * V[s_next]
V_new[s] = reward + gamma * future_value
delta = max(delta, abs(V_new[s] - V[s]))
V = V_new.copy()
if delta < theta:
break
# Policy Improvement
policy_stable = True
for s in range(n_states):
old_action = policy[s]
# Calculate Q-values for all actions
Q = np.zeros(n_actions)
for a in range(n_actions):
reward = r(s, a)
future_value = 0
for s_next in range(n_states):
future_value += P[s][a][s_next] * V[s_next]
Q[a] = reward + gamma * future_value
best_action = np.argmax(Q)
policy[s] = best_action
if old_action != best_action:
policy_stable = False
if policy_stable:
break
return V, policy
Monte Carlo Learning
根据大数定律,通过足够次数的采样实验,数据期望会接近理想模型期望,从而用数据替代模型,状态价值是,动作价值也是 !
$$ Q^{\pi}(s,a) = \mathbb{E}_\pi[G_t∣S_t = s, A_t = a] \approx \frac{1}{N}\sum^{N}_{i=1}g^{(i)}(s,a) \\ \text{where g(s,a) is a sample of } G_t $$- 策略评估:基于给定 $\pi$,对任一 $(s,a)$ 多次采样得到足够多条足够长”经验轨迹“ $\mathbf{q}_\pi(s,a)$
- 策略优化:计算$$\mathbf{q}_\pi$$的各项$\mathbb{E}[\mathbf{q}_\pi(s,a)]$,最大项对应优化的策略 $\pi^{'} = \arg\max_{\pi} ( \pi(a|s) Q^{\pi}(s,a))$
- 迭代1,2直到策略稳定
# MC Basic
num_episodes = 100
policy = np.random.choice(n_actions, size=n_states)
while True:
policy_stable = True
# MC Policy Evaluation
for s in range(n_states):
old_action = policy[s]
# Calculate Q-values for all actions
Q = np.zeros(n_actions)
for a in range(n_actions):
Q[a] += avg_q_from_samples(s,a,num_episodes)
# Policy Improvement
best_action = np.argmax(Q)
policy[s] = best_action
if old_action != best_action:
policy_stable = False
if policy_stable:
break
V = np.zeros(n_states)
for s in range(n_states):
V[s] = np.max(Q[s])
return V, policy
单条”经验轨迹“可以作为轨迹上任一 $(s,a)$不同长度的采样,除了已访问$(s,a)$!
由于优化方向一致,任意条”经验轨迹“都可以用于增量式策略优化!
# MC Exploring Starts
episodes_history
policy = np.random.choice(n_actions, size=n_states)
Q = np.zeros((n_states, n_actions))
returns = {}
# Policy Evaluation
for episode_history in episodes_history:
# Calculate Q-values for all actions
G = 0
visited = set()
for t in range(len(episode_history)-1, -1, -1):
state, action, reward = episode_history[t]
state_action = (state, action)
G = reward + gamma * G
if state_action not in visited:
visited.add(state_action)
if state_action not in returns:
returns[state_action] = []
returns[state_action].append(G)
Q[state, action] = np.mean(returns[state_action])
# Policy Improvement
for s in range(n_states):
best_action = np.argmax(Q[s])
policy[s] = best_action
V = np.zeros(n_states)
for s in range(n_states):
V[s] = np.max(Q[s])
return V, policy
我们要保证所有$(s,a)$都有采样,那么我们至少要求存在任一$(s,a)$开始的”经验轨迹“,但如果对任一状态的动作是基于概率的随机采样,那么只要”经验轨迹“足够长,就一定能以较少的”经验轨迹“中找到任一$(s,a)$开始的”经验轨迹“
$$ \pi(a|s) = \begin{cases} 1 - \varepsilon + \dfrac{\varepsilon}{|\mathcal{A}(s)|} & \text{if } a = \arg\max_{a'} Q(s,a') \\ \dfrac{\varepsilon}{|\mathcal{A}(s)|} & \text{otherwise} \end{cases} $$- $\xi$:与最优性呈反相关,与探索性呈正相关
# MC xi-Greedy
xi = 0.1
episodes_history
policy = np.random.choice(n_actions, size=n_states)
Q = np.zeros((n_states, n_actions))
returns = {}
# Policy Evaluation
for episode_history in episodes_history:
# Calculate Q-values for all actions
G = 0
for t in range(len(episode_history)-1, -1, -1):
state, action, reward = episode_history[t]
state_action = (state, action)
G = reward + gamma * G
if state_action not in returns:
returns[state_action] = []
returns[state_action].append(G)
Q[state, action] = np.mean(returns[state_action])
# ε-greedy Policy Improvement
for s in range(n_states):
if np.random.random() > epsilon:
best_action = np.argmax(Q[s])
policy[s] = best_action
else:
policy[s] = np.random.choice(n_actions)
V = np.zeros(n_states)
for s in range(n_states):
V[s] = np.max(Q[s])
return V, policy
Stochastic Approximation
Incremental Avg
$$ \begin{align*} w_{k+1} &= \frac{1}{k} \sum_{i=1}^{k} x_{i} \\ &= \frac{1}{k} \left( \sum_{i=1}^{k-1} x_{i} + x_{k} \right) \\ &= \frac{1}{k} \left( (k-1) \cdot w_{k} + x_{k} \right) \\ &= w_k - \frac{1}{k} \left( w_k - x_{k}\right) \end{align*} $$Eobbins-Monro
近似找到一个参数 $w$,使得某个黑盒模型 $g(w)=0$ ,可通过采样获取带噪音的测量值 $\overset{\sim}{g}(w_k, \eta_k)=g(w_k) + \eta_k$,下面是一个迭代的随机逼近过程:
$$ w_{k+1} = w_k - \alpha_k \cdot \tilde{g}(w_k, \eta_k) $$- $\sum_{k=1}^{\infty} \alpha_k = \infty, \sum_{k=1}^{\infty} \alpha_k^2 < \infty$:学习率缓慢衰减到0,以保证$w$的收敛,如$\frac{1}{k}$或$\frac{1}{k^2}$
- $0 < \nabla g(w) \leq c_2$ :黑盒模型递增,且梯度有界以防发散
- $\mathbb{E}[\eta_k | w_k] = 0, \quad \mathbb{E}[\eta_k^2 | w_k] < \infty$:噪声可被平均抵消,其中异常不会过分偏大
GD
最优化问题,令$f(w, X)$为凸函数,$\alpha_k$总合适:
$$ \begin{align*} &\underset{w}{\min} \, J(w) = \mathbb{E}[f(w, X)] \rightarrow \nabla_w \mathbb{E}[f(w, X)] = 0 \rightarrow \nabla_w f(w, \mathbb{E}[X]) \\ &\textbf{GD:} \quad w_{k+1} = w_k - \alpha_k \nabla_w \mathbb{E} [f(w_k, X_k)] = w_k - \alpha_k \mathbb{E} [\nabla_w f(w_k, X_k)] \\ &\textbf{BGD:} \quad w_{k+1} = w_k - \alpha_k \frac{1}{n} \sum_{i=1}^{n} \nabla_w f(w_k, x_i) \\ &\textbf{MBGD:} \quad w_{k+1} = w_k - \alpha_k \frac{1}{m} \sum_{j \in I_x} \nabla_w f(w_k, x_j) \\ &\textbf{SGD:} \quad w_{k+1} = w_k - \alpha_k \nabla_w f(w_k, x_k) \end{align*} $$具有靠近快速收敛,接近随机收敛的特性。同时,MBGD采样需要可重复随机,通过 batch 的方式消除噪音对收敛的干扰!
Norm-Incremental Avg
求$\mathbb{E}[X]$,令$g(w)=w-\mathbb{E}[X]$,则:
$$ \overset{\sim}{g}(w, \eta)= w - x = g(w) + (\mathbb{E}[X] - x) = g(w) + \eta \rightarrow \\ w_{k+1} = w_k - \alpha_k \left( w_k - x_k\right) $$使得 $w$ 会朝 $\mathbb{E}[X]$ 收敛;
通过SGD,令$f(w, X)=\frac{1}{2}||w-\mathbb{E}[x]||^2=\frac{1}{2n} \sum_{i=1}^{n}||w-x_i||^2$,也会得到相同的结论。
Temporal-Difference Learning
对于一个无模型的环境,我们需要求解贝尔曼方程状态价值(由于这里是基于数据,$\mathbf{P}_\pi$已被融入$v_\pi$的计算中):
$$ v_\pi(s) = \mathbb{E}[R_\pi + \gamma v_\pi(S')|s] $$令$g(v(s))=v(s)-\mathbb{E}[R_\pi + \gamma v_\pi(S')|s]$,则:
$$ \overset{\sim}{g}(v(s), \eta)= v(s) - (r_\pi + \gamma v_\pi(s')) = g(v(s)) + (\mathbb{E}[R_\pi + \gamma v_\pi(S')|s] - (r_\pi + \gamma v_\pi(s'))) = g(v(s)) + \eta \rightarrow \\ \begin{cases} v_{t+1}(s) = v_t(s) - \alpha_t \left( v_t(s) - (r_{t+1} + \gamma v_t(s')))\right) \\ v_{t+1}(s) = v_t(s) \quad \forall s \notin \text{episode} \end{cases} $$使得 $v(s)$ 会朝 $\mathbb{E}[R_\pi + \gamma v_\pi(S')|s]$ 收敛,即$v(s)=v_\pi(s)$:
- $r_{t+1} + \gamma v_t(s')$:TD target($\bar{v}_{t}$),t 时刻状态s收敛方向
- $v_t(s) - (r_{t+1} + \gamma v_t(s'))$:TD error($\sigma_t$),t 时刻状态s与实际采样差距
| 特性 | MC(离线) | TD(在线) |
|---|---|---|
| 更新时机 | 回合结束后(离线) | 每一步之后(在线) |
| 核心方法 | 使用实际回报$G_t$ | 自举,使用估计值 $r_{t+1} + \gamma v_t(s')$ |
| 偏差/方差 | 无偏,高方差,收敛性好 | 有偏,低方差,收敛快,依赖初始估计 |
| 应用场景 | 回合制任务 | 持续型任务 |
Sarsa
对于一个无模型的环境,我们需要求解贝尔曼方程动作价值:
$$ q_\pi(s,a) = \mathbb{E}[R_\pi + \gamma q_\pi(S',A')|s,a] $$令$g(q(s,a))=q(s,a)-\mathbb{E}[R_\pi + \gamma q_\pi(S',A')|s,a]$,则:
$$ \overset{\sim}{g}(q(s,a), \eta)= q(s,a) - (r_\pi + \gamma q_\pi(s',a')) = g(q(s,a)) + (\mathbb{E}[R_\pi + \gamma q_\pi(S',A')|s,a] - (r_\pi + \gamma q_\pi(s',a'))) = g(v(s)) + \eta \rightarrow \\ \begin{cases} q_{t+1}(s,a) = q_t(s,a) - \alpha_t \left( q_t(s,a) - (r_{t+1} + \gamma q_t(s',a'))\right) \\ q_{t+1}(s,a) = q_t(s,a) \quad \forall (s,a) \notin \text{episode} \end{cases} $$使得 $q(s,a)$ 会朝 $\mathbb{E}[R_\pi + \gamma q_\pi(S',A')|s,a]$ 收敛,即$q(s,a)=q_\pi(s,a)$,
接下来策略优化,基于预估$q(s,a)$,最大项对应优化的策略 $\pi^{'} = \arg\max_{\pi} ( \pi(a|s) Q^{\pi}(s,a))$
def get_best_action(state):
# ε-greedy Policy Improvement
if np.random.random() > epsilon:
best_action = np.argmax(Q[state])
else:
best_action = np.random.choice(n_actions)
return best_action
trajectory = []
total_reward = 0
Q = np.zeros((n_states, n_actions))
cur_state = start_state
cur_action = get_best_action(cur_state)
trajectory.append(0, cur_state, cur_action)
while cur_state is not target_state:
reward = r(cur_state, cur_action)
next_state = np.random.choice(n_states, p=P[cur_state][cur_action])
next_action = get_best_action(next_state)
total_reward += reward
trajectory.append(reward,next_state, next_action)
# TD Policy Evaluation
Q[cur_state][cur_action] = Q[cur_state][cur_action] + alpha * (reward + gamma * Q[next_state][next_action] - Q[cur_state][cur_action])
cur_state, cur_action = next_state, next_action
policy = np.argmax(Q, axis=1)
V = np.zeros(n_states)
for s in range(n_states):
V[s] = np.max(Q[s])
return V, policy
我们注意到,求解贝尔曼方程动作价值应该为:
$$ q_\pi(s,a) = \mathbb{E}[R_\pi + \gamma \mathbb{E}[q_\pi(S',A)|s]] $$进而原动作价值评估迭代变为:
$$ \begin{cases} q_{t+1}(s,a) = q_t(s,a) - \alpha_t \left( q_t(s,a) - (r_{t+1} + \gamma \mathbb{E}[q_t(s',A)])\right) \\ q_{t+1}(s,a) = q_t(s,a) \quad \forall (s,a) \notin \text{episode} \end{cases} $$def get_best_action(state):
# ε-greedy Policy Improvement
if np.random.random() > epsilon:
action = np.argmax(Q[state])
else:
action = np.random.choice(n_actions)
return action
def get_expected_q_value(state):
# Expected Q
best_action = np.argmax(Q[state])
action_probs = np.ones(n_actions) * (epsilon / n_actions)
action_probs[best_action] += (1 - epsilon)
expected_value = 0
for a in range(n_actions):
expected_value += action_probs[a] * Q[state][a]
return expected_value
trajectory = []
total_reward = 0
Q = np.zeros((n_states, n_actions))
cur_state = start_state
cur_action = get_best_action(cur_state)
trajectory.append(0, cur_state, cur_action)
while cur_state is not target_state:
reward = r(cur_state, cur_action)
next_state = np.random.choice(n_states, p=P[cur_state][cur_action])
next_action = get_best_action(next_state)
total_reward += reward
trajectory.append(reward,next_state, next_action)
# TD Policy Evaluation
Q[cur_state][cur_action] = Q[cur_state][cur_action] + alpha * (reward + gamma * get_expected_q_value(next_state) - Q[cur_state][cur_action])
cur_state, cur_action = next_state, next_action
policy = np.argmax(Q, axis=1)
V = np.zeros(n_states)
for s in range(n_states):
V[s] = np.max(Q[s])
return V, policy
考虑n时间步,求解贝尔曼方程动作价值:
$$ q_\pi(s,a) = \mathbb{E}[R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1} R_{t+n} + \gamma^n q_\pi(S^{n'},A^{n'})|s,a] $$进而原动作价值评估迭代变为:
$$ \begin{cases} q_{t-n+1}(s, a) = q_{t-n}(s, a) - \alpha_{t-n} \left( q_{t-n}(s, a) - (r_{t-n+1} + \gamma r_{t-n+2} + \cdots + \gamma^{n-1} r_{t} + \gamma^n q_{t-n}(s^{n'},a^{n'})) \right) \\ q_{t-n+1}(s, a) = q_{t-n}(s, a) - \alpha_{t-n} \left( q_{t-n}(s, a) - (r_{t-n+1} + \gamma r_{t-n+2} + \cdots + \gamma^{n-k} r_{t-k+1} \right) \quad \nexists s^{n'},a^{n'} \end{cases} $$def get_best_action(state):
# ε-greedy Policy Improvement
if np.random.random() > epsilon:
best_action = np.argmax(Q[state])
else:
best_action = np.random.choice(n_actions)
return best_action
trajectory = []
total_reward = 0
Q = np.zeros((n_states, n_actions))
cur_state = start_state
cur_action = get_best_action(cur_state)
trajectory.append(0, cur_state, cur_action)
n_steps
experience_buffer = []
while cur_state is not target_state:
reward = r(cur_state, cur_action)
next_state = np.random.choice(n_states, p=P[cur_state][cur_action])
next_action = get_best_action(next_state)
total_reward += reward
trajectory.append(reward,next_state, next_action)
# n-steps
experience = (cur_state, cur_action, reward)
experience_buffer.append(experience)
# TD Policy Evaluation
if len(experience_buffer) >= n_steps:
n_step_ago_state, n_step_ago_action, n_step_reward = experience_buffer[0]
n_step_return = 0
for i in range(len(experience_buffer)):
n_step_return += (gamma ** i) * experience_buffer[i][2]
if next_state is not target_state:
n_step_return += (gamma ** n_steps) * Q[next_state][next_action]
Q[n_step_ago_state][n_step_ago_action] = Q[n_step_ago_state][n_step_ago_action] + alpha * (n_step_return - Q[n_step_ago_state][n_step_ago_action])
experience_buffer.pop(0)
cur_state, cur_action = next_state, next_action
# left n-steps
while len(experience_buffer) > 0:
n_step_ago_state, n_step_ago_action, n_step_reward = experience_buffer[0]
n_step_return = 0
for i in range(len(experience_buffer)):
n_step_return += (gamma ** i) * experience_buffer[i][2]
Q[n_step_ago_state][n_step_ago_action] = Q[n_step_ago_state][n_step_ago_action] + alpha * (
n_step_return - Q[n_step_ago_state][n_step_ago_action]
)
experience_buffer.pop(0)
policy = np.argmax(Q, axis=1)
V = np.zeros(n_states)
for s in range(n_states):
V[s] = np.max(Q[s])
return V, policy
Q-learning
作为Sarsa及其Eexcepted形式的折中,可以在价值估计时进行策略优化,求解贝尔曼最优方程动作价值:
进而原动作价值评估迭代变为:
$$ \begin{cases} q_{t+1}(s,a) = q_t(s,a) - \alpha_t \left( q_t(s,a) - (r_{t+1} + \gamma \underset{a' \in A}{max}q_t(s_{t+1},a'))\right) \\ q_{t+1}(s,a) = q_t(s,a) \quad \forall (s,a) \notin \text{episode} \end{cases} $$| 特性 | Q-learning(心大) | Sarsa(谨慎) |
|---|---|---|
| 更新时机 | 回合结束后(离线) | 每一步之后(在线) |
| 更新方式 | off-policy,理想最优路径,只看下一步最好的可能 | on-policy,实际行走路径,看下一步实际要走的 |
| 结果 | 更冒险,但可能更快 | 更具探索性,更安全,会避开危险 |
| 打个比方 | 规划路线时,只算最短距离 | 规划路线时,会把坑洼路段也考虑进去 |
- policy
- behavior policy:和环境交互并采集数据的策略
- target policy:算法评估和改进的策略
# Q-learning off-policy
episodes_history
Q = np.zeros((n_states, n_actions))
# Policy Evaluation
for episode_history in episodes_history:
for t in range(len(episode_history)-1):
state, action, reward = episode_history[t]
next_state, next_action, next_reward = episode_history[t+1]
if t == len(episode_history)-2:
q_target = reward + gamma * next_reward
else:
q_target = reward + gamma * np.max(Q[next_state])
Q[state, action] = Q[state, action] + alpha * (q_target - Q[state, action])
# Policy Improvement
policy = np.random.choice(n_actions, size=n_states)
for s in range(n_states):
best_action = np.argmax(Q[s])
policy[s] = best_action
V = np.zeros(n_states)
for s in range(n_states):
V[s] = np.max(Q[s])
return V, policy
sum
$$ \begin{array}{l} q_{t+1}(s_{t},a_{t})=q_{t}(s_{t},a_{t})-\alpha_{t}(s_{t},a_{t})[q_{t}(s_{t},a_{t})-\tilde{q}_{t}], \end{array} $$| Algorithm | TD target $\tilde{q}_{t}$ | Equation to be solved |
|---|---|---|
| Sarsa | $r_{t+1}+\gamma q_{t}(s_{t+1},a_{t+1})$ | $q_{\pi}(s,a)=\mathbb{E}[R_{t+1}+\gamma q_{\pi}(S_{t+1},A_{t+1}) |
| n-step Sarsa | $r_{t+1}+\gamma r_{t+2}+\cdots+\gamma^{n}q_{t}(s_{t+n},a_{t+n})$ | $q_{\pi}(s,a)=\mathbb{E}[R_{t+1}+\gamma R_{t+2}+\cdots+\gamma^{n}q_{\pi}(S_{t+n},A_{t+n}) |
| Q-learning | $r_{t+1}+\gamma\max_{a}q_{t}(s_{t+1},a)$ | $q(s,a)=\mathbb{E}[R_{t+1}+\gamma\max_{a}q(S_{t+1},a) |
| Monte Carlo | $r_{t+1}+\gamma r_{t+2}+\gamma^{2}r_{t+3}+\ldots$ | $q_{\pi}(s,a)=\mathbb{E}[R_{t+1}+\gamma R_{t+2}+\gamma^{2}R_{t+3}+\ldots |
如何处理连续性状态空间?参数拟合 减少存储,加强泛化(将噪音局部扩散)
Value Function Approximation
拟合状态价值函数,减小(带状态权重的)状态价值损失函数:
$$ J(w) = \sum_{s \in S}d_\pi(s)(v_\pi(s) - \hat{v}(s,w))^2 \\ d_\pi(s) = \frac{n_\pi(s)}{\sum_{s' \in S}n_\pi(s')} \\ d^T_\pi = d^T_\pi P_\pi $$梯度下降优化:
$$ w_{t+1} = w_{t} - \alpha_t \nabla_wJ(w_t) = w_{t} + \alpha_t (v_\pi(s_t) - \hat{v}(s_t,w_t)) \nabla_w\hat{v}(s_t,w_t) $$其中,$v_\pi(s_t)$未知,可通过MC或者TD估计:
$$ \begin{align*} &\textbf{MC:} \quad w_{t+1} = w_{t} + \alpha_t (g_t - \hat{v}(s_t,w_t)) \nabla_w\hat{v}(s_t,w_t) \\ &\textbf{TD:} \quad w_{t+1} = w_{t} + \alpha_t (r_{t+1}+\gamma \hat{v}(s_{t+1},w_t) - \hat{v}(s_t,w_t)) \nabla_w\hat{v}(s_t,w_t) \end{align*} $$$\hat{v}(s,w)$具有多种对状态价值的拟合函数,主流是神经网络!
DQN
$$ J(w) = \mathbb{E} \left[ (R + \gamma \underset{a \in A(S')}{max} \hat{q}(S',a,w_T) - \hat{q}(S,a,w))^2 \right] \\ \nabla_wJ(w) = \mathbb{E} \left[ (R + \gamma \underset{a \in A(S')}{max} \hat{q}(S',a,w_T) - \hat{q}(S,a,w)) \nabla_w\hat{q}(S,a,w) \right] $$双网络架构
- 主网络($\hat{q}(s,a,w)$)为当前正在训练的网络,用于生成动作选择
- 目标网络($\hat{q}(s,a,w_T)$)相对固定,用于计算TD目标,初始时与主网络相同
经验回放缓冲
- 使用主网络与环境交互,生成样本,存入缓冲区$(s,a,r,s')$
- 采样最小化目标网络的TD目标与主网络估计值的差距
- 主网络赋值给目标网络
# DQN off-policy
class DQN(nn.Module):
def __init__(self, input_dim, output_dim):
super().__init__()
self.fc1 = nn.Linear(input_dim, 128)
self.fc2 = nn.Linear(128, 128)
self.fc3 = nn.Linear(128, output_dim)
def forward(self, x):
x1 = torch.relu(self.fc1(x))
x2 = torch.relu(self.fc2(x1))
return self.fc3(x2)
class DQNAgent:
def __init__(self, state_dim, action_dim, learning_rate, gamma):
self.state_dim = state_dim
self.action_dim = action_dim
# Initialize main network and target network
self.q_network = DQN(state_dim, action_dim)
self.target_network = DQN(state_dim, action_dim)
self.target_network.load_state_dict(self.q_network.state_dict())
self.optimizer = optim.Adam(self.q_network.parameters(), lr=learning_rate)
self.batch_size = 32
self.memory_size = 10000
self.memory = deque(maxlen=self.memory_size)
self.learning_step = 0
self.target_update_freq = 100
def get_best_action(self, state):
# ε-greedy Policy Improvement for nn
if np.random.random() > epsilon:
with torch.no_grad():
state_tensor = torch.FloatTensor(state).unsqueeze(0)
q_values = self.q_network(state_tensor)
best_action = np.argmax(q_values.numpy())
else:
best_action = np.random.choice(self.action_dim)
return best_action
def store_experience(self, state, action, reward, next_state, done):
self.memory.append((state, action, reward, next_state, done))
def update_network(self):
if len(self.memory) < self.batch_size:
return
# Sample batch from experience replay
batch = random.sample(self.memory, self.batch_size)
states, actions, rewards, next_states, dones = zip(*batch)
states = torch.FloatTensor(states)
actions = torch.LongTensor(actions).unsqueeze(1)
rewards = torch.FloatTensor(rewards)
next_states = torch.FloatTensor(next_states)
dones = torch.BoolTensor(dones)
# Current Q values
current_q_values = self.q_network(states).gather(1, actions).squeeze()
# TD target
with torch.no_grad():
next_q_values = self.target_network(next_states).max(1)[0]
# Set Q value to 0 for terminal states
next_q_values[dones] = 0.0
target_q_values = rewards + gamma * next_q_values
# Gradient Descent
loss = nn.MSELoss()(current_q_values, target_q_values)
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
# Update target network periodically
self.learning_step += 1
if self.learning_step % self.target_update_freq == 0:
self.target_network.load_state_dict(self.q_network.state_dict())
return loss.item()
def train_dqn(env, n_episodes=1000):
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = DQNAgent(state_dim, action_dim,learning_rate, gamma)
for episode in range(n_episodes):
total_reward = 0
# Environment reset
cur_state = env.reset()
cur_action = agent.get_best_action(cur_state)
done = False
step_count = 0
while not done:
# Take action and observe next state and reward
next_state, reward, done, truncated, _ = env.step(cur_action)
next_action = agent.get_best_action(next_state)
total_reward += reward
done = done or truncated
agent.store_experience(cur_state, cur_action, reward, next_state, done)
loss = agent.update_network()
cur_state, cur_action = next_state, next_action
step_count += 1
if episode % 100 == 0:
print(f"Episode {episode}, Total Reward: {total_reward:.2f}, Steps: {step_count}, Loss: {loss}")
return agent
起始的策略最好是均等动作概率,以加强探索性!!!
Policy Gradient Methods
拟合动作策略函数,提升累计折扣回报:
$$ J(\theta) = \overline{v}_\pi = \sum_{s \in S}d_\pi(s)v_\pi(s) = \sum_{s \in S}d_\pi(s) (r_\pi(s) + \gamma v_\pi(s')) = \mathbb{E} [ \sum_{t=0}^{\infty}\gamma^t R_{t+1} ]\\ d_\pi(s) = \frac{n_\pi(s)}{\sum_{s' \in S}n_\pi(s')} \\ d^T_\pi = d^T_\pi P_\pi $$梯度上升优化:
$$ \nabla_\theta J(\theta) \cong \sum_{s \in S} \eta(s) \sum_{a \in A} \nabla_\theta \pi(a|s,\theta)q_\pi(s,a) = \mathbb{E}_{S\sim\eta,A\sim\pi} [ \nabla_\theta \ln \pi(A|S,\theta)q_\pi(S,A) ]\\ \theta_{t+1} = \theta_{t} + \alpha_t \nabla_\theta J(\theta_t) = \theta_{t} + \alpha_t \nabla_\theta \ln \pi(a_t|s_t,\theta_t)q_\pi(s_t,a_t) \\ \theta_{t+1} = \theta_{t} + \alpha_t \nabla_\theta J(\theta_t) = \theta_{t} + \alpha_t \frac{q_\pi(s_t,a_t)}{\pi(a_t|s_t,\theta_t)} \nabla_\theta \pi(a_t|s_t,\theta_t) $$平衡探索与利用!
如果之前数据中表现出较大的$q(s,a)$,则会加强这种动作,加强利用
如果之前数据中表现出较小的$\pi(a_t|s_t,\theta_t)$,则会加强这种动作,加强探索
其中,$q_\pi(s_t,a_t)$未知,可通过MC或者TD估计:
$$ \begin{align*} &\textbf{MC:} \quad \theta_{t+1} = \theta_{t} + \alpha_t \nabla_\theta \ln \pi(a_t|s_t,\theta_t)g_t \\ &\textbf{TD:} \quad \theta_{t+1} = \theta_{t} + \alpha_t \nabla_\theta \ln \pi(a_t|s_t,\theta_t)(r_{t+1}+\gamma q_\pi(s_{t+1}, a_{t+1})) \end{align*} $$REINFORCE
MC估计
# REINFORCE on policy
class PolicyNetwork(nn.Module):
def __init__(self, input_dim, output_dim):
super().__init__()
self.fc1 = nn.Linear(input_dim, 128)
self.fc2 = nn.Linear(128, 128)
self.fc3 = nn.Linear(128, output_dim)
def forward(self, x):
x1 = torch.relu(self.fc1(x))
x2 = torch.relu(self.fc2(x1))
# Use softmax to output action probabilities
return torch.softmax(self.fc3(x2), dim=-1)
class REINFORCEAgent:
def __init__(self, state_dim, action_dim, learning_rate, gamma):
self.state_dim = state_dim
self.action_dim = action_dim
# Initialize policy network
self.policy_network = PolicyNetwork(state_dim, action_dim)
self.optimizer = optim.Adam(self.policy_network.parameters(), lr=learning_rate)
self.trajectory = []
def get_best_action(self, state, training=True):
state_tensor = torch.FloatTensor(state).unsqueeze(0)
action_probs = self.policy_network(state_tensor)
if training:
# Sample action from probability distribution during training
action_dist = torch.distributions.Categorical(action_probs)
action = action_dist.sample()
log_prob = action_dist.log_prob(action)
return action.item(), log_prob
else:
# Use greedy action during evaluation
return torch.argmax(action_probs).item(), None
def get_policy(self, states):
"""Extract policy"""
policy = []
with torch.no_grad():
for state in states:
state_tensor = torch.FloatTensor(state).unsqueeze(0)
action_probs = self.policy_network(state_tensor).numpy()[0]
best_action = np.argmax(action_probs)
policy.append(best_action)
return np.array(policy)
def store_transition(self, state, action, log_prob, reward, done):
self.trajectory.append((state, action, log_prob, reward, done))
def update_policy(self):
if not self.trajectory:
return 0
*_, log_probs, rewards, _ = zip(*self.trajectory)
# Caculate returns
returns = []
G = 0
for r in reversed(rewards):
G = r + gamma * G
returns.insert(0, G)
returns = torch.FloatTensor(returns)
returns = (returns - returns.mean()) / (returns.std() + 1e-8)
log_probs = torch.stack(log_probs)
# Gradient Rise
loss = (-log_probs * returns).mean()
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
self.trajectory = []
return loss.item()
def train_reinforce(env, n_episodes=1000):
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = REINFORCEAgent(state_dim, action_dim, learning_rate, gamma)
for episode in range(n_episodes):
total_reward = 0
# Environment reset
state = env.reset()
done = False
step_count = 0
while not done:
action, log_prob = agent.get_best_action(state)
next_state, reward, done, truncated, _ = env.step(action)
total_reward += reward
done = done or truncated
agent.store_transition(state, action, log_prob, reward, done)
loss = agent.update_policy()
state = next_state
step_count += 1
if episode % 100 == 0:
print(f"Episode {episode}, Total Reward: {total_reward:.2f}, Steps: {step_count}, Loss: {loss}")
return agent
Actor-Critic Methods
QAC
一个网络用于评估动作价值,一个网络用于提升动作价值
critic:policy evaluation 降低 TD error,以此估计$q_\pi(s_t,a_t,w_t)$
$$ w_{t+1} = w_{t} + \alpha_t (r_{t+1}+\gamma q(s_{t+1},a_{t+1},w_t) - q(s_t,a_t,w_t)) \nabla_w q(s_t,a_t,w_t) $$actor:policy update 提升价值或奖励估计
$$ \theta_{t+1} = \theta_{t} + \alpha_t \nabla_\theta \ln \pi(a_t|s_t,\theta_t)q_\pi(s_t,a_t,w_t) $$
A2C
指标梯度添加偏置对优化不产生影响,因此我们希望添加优势函数估计$A(s,a)=Q(s,a) -V(s)$:
$$ \nabla_\theta J(\theta) \cong \mathbb{E}_{S\sim\eta,A\sim\pi} [ \nabla_\theta \ln \pi(A|S,\theta)q_\pi(S,A) ]= \mathbb{E}_{S\sim\eta,A\sim\pi} [ \nabla_\theta \ln \pi(A|S,\theta)(q_\pi(S,A) - b(S))] $$但方差会因为采样产生变动,下面的baseline会使得方差最小:
$$ b^*(S) = \frac{\mathbb{E}_{A \sim \pi} \left[ \|\nabla_\theta \ln \pi(A|s,\theta_t)\|^2 \cdot q(s,A) \right]}{\mathbb{E}_{A \sim \pi} \left[ \|\nabla_\theta \ln \pi(A|s,\theta_t)\|^2 \right]} $$过于复杂,实际上采用:
$$ b'(s)= \mathbb{E}_{A \sim \pi}[q(s,A)]=v_\pi(s) $$因此,actor 变为带的形式:
$$ \theta_{t+1} = \theta_{t} + \alpha_t \nabla_\theta \ln \pi(a_t|s_t,\theta_t)(q_\pi(s_t,a_t,w_t) - v_\pi(s)) $$只考虑某次迭代中同状态不同动作价值之间的相对性,从而减小了迭代优化过程中的强抖动
最后,合并critic可以减少一个神经网络:
$$ \theta_{t+1} = \theta_{t} + \alpha_t \nabla_\theta \ln \pi(a_t|s_t,\theta_t)(r_{t+1}+\gamma q(s_{t+1},a_{t+1},w_t) - v_\pi(s)) $$# A2C on policy
class ActorCriticNetwork(nn.Module):
def __init__(self, input_dim, output_dim):
super().__init__()
# Shared feature extraction layers
self.shared_fc1 = nn.Linear(input_dim, 128)
self.shared_fc2 = nn.Linear(128, 128)
# Actor head - outputs action probabilities
self.actor_fc = nn.Linear(128, output_dim)
# Critic head - outputs state value
self.critic_fc = nn.Linear(128, 1)
def forward(self, x):
x1 = torch.relu(self.shared_fc1(x))
x2 = torch.relu(self.shared_fc2(x1))
# Actor output: action probabilities
action_probs = torch.softmax(self.actor_fc(x2), dim=-1)
# Critic output: state value
state_value = self.critic_fc(x2)
return action_probs, state_value
class A2CAgent:
def __init__(self, state_dim, action_dim, learning_rate, gamma):
self.state_dim = state_dim
self.action_dim = action_dim
self.entropy_coef = 0.01
# Initialize actor-critic network
self.network = ActorCriticNetwork(state_dim, action_dim)
self.optimizer = optim.Adam(self.network.parameters(), lr=learning_rate)
self.trajectory = []
def get_best_action(self, state, training=True):
state_tensor = torch.FloatTensor(state).unsqueeze(0)
action_probs, state_value = self.network(state_tensor)
if training:
# Sample action from probability distribution during training
action_dist = torch.distributions.Categorical(action_probs)
action = action_dist.sample()
log_prob = action_dist.log_prob(action)
entropy = action_dist.entropy()
return action.item(), log_prob, entropy, state_value.squeeze()
else:
# Use greedy action during evaluation
return torch.argmax(action_probs).item(), None, None, state_value.squeeze()
def get_policy(self, states):
"""Extract policy"""
policy = []
with torch.no_grad():
for state in states:
state_tensor = torch.FloatTensor(state).unsqueeze(0)
action_probs, _ = self.network(state_tensor)
action_probs = action_probs.numpy()[0]
best_action = np.argmax(action_probs)
policy.append(best_action)
return np.array(policy)
def store_transition(self, state, action, log_prob, entropy, value, reward, done):
self.trajectory.append((state, action, log_prob, entropy, value, reward, done))
def update_policy(self):
if not self.trajectory:
return 0, 0, 0
states, *_, log_probs, entropies, values, rewards, dones = zip(*self.trajectory)
# Calculate advantages and returns
advantages = []
returns = []
G = 0
for i in reversed(range(len(rewards))):
G = rewards[i] + gamma * G * (1 - dones[i])
returns.insert(0, G)
advantages.insert(0, G - values[i])
advantages = torch.FloatTensor(advantages)
advantages = (advantages - advantages.mean()) / (advantages.std() + 1e-8)
returns = torch.FloatTensor(returns)
log_probs = torch.stack(log_probs)
values_tensor = torch.stack(values)
entropies = torch.stack(entropies)
# Calculate Rise
actor_loss = (-log_probs * advantages.detach()).mean()
# actor_loss_off_policy = (-(self.network(states)/log_probs)*(log_probs * advantages.detach())).mean()
critic_loss = 0.5 * (returns - values_tensor).pow(2).mean()
entropy_loss = -entropies.mean()
total_loss = actor_loss + critic_loss + self.entropy_coef * entropy_loss
self.optimizer.zero_grad()
total_loss.backward()
torch.nn.utils.clip_grad_norm_(self.parameters(), max_norm=0.5)
self.optimizer.step()
self.trajectory = []
return actor_loss.item(), critic_loss.item(), entropy_loss.item()
def train_a2c(env, n_episodes=1000):
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = A2CAgent(state_dim, action_dim, learning_rate, gamma)
for episode in range(n_episodes):
total_reward = 0
# Environment reset
state = env.reset()
done = False
step_count = 0
while not done:
action, log_prob, entropy, value = agent.get_best_action(state)
next_state, reward, done, truncated, _ = env.step(action)
total_reward += reward
done = done or truncated
agent.store_transition(state, action, log_prob, entropy, value, reward, done)
actor_loss, critic_loss, entropy_loss = agent.update_policy()
state = next_state
step_count += 1
if episode % 100 == 0:
print(f"Episode {episode}, Total Reward: {total_reward:.2f}, Steps: {step_count}")
print(f" Actor Loss: {actor_loss:.4f}, Critic Loss: {critic_loss:.4f}, Entropy Loss: {entropy_loss:.4f}")
def test_a2c(env, agent):
state = env.reset()
done = False
total_reward = 0
while not done:
action, _, _, _ = agent.get_best_action(state, training=False)
next_state, reward, done, truncated, _ = env.step(action)
done = done or truncated
total_reward += reward
state = next_state
print(f"Test Reward: {total_reward}")
importance sampling
如何off policy?
behavior policy 与 target policy 采样服从不同的分布,我们希望找到不同策略下样本之间的关系,使得通过该关系,从behavior policy得到的分布会趋向 target policy
$$ \bar{x} = \frac{1}{n}\sum_{i=1}^{n}x_i \rightarrow \mathbb{R}_{X\sim p_1}[X] \\ \bar{f} = \frac{1}{n}\sum_{i=1}^{n}\frac{p_0(x_i)}{p_1(x_i)}x_i \rightarrow \mathbb{R}_{X\sim p_0}[X] $$将 p1分布的采样转移到p0分布上,使其均值一致,本质上就是一个加权平均。
$$ J(\theta) = \sum_{s \in S}d_\beta(s)v_\pi(s) \\ \nabla_\theta J(\theta) \cong \mathbb{E}_{S\sim\rho,A\sim\pi} [ \frac{\pi(A|S,\theta)}{\beta(A|S)} \nabla_\theta \ln \pi(A|S,\theta)q_\pi(S,A) ] \\ \theta_{t+1} = \theta_{t} + \alpha_t \frac{\pi(a_t|s_t, \theta_t)}{\beta(a_t|s_t)} \nabla_\theta \ln\pi(a_t|s_t,\theta_t)(q_t(s_t,a_t)-v_t(s_t)) $$
即在更新梯度时存在关于两个神经网络关于概率的分布的权重转换
如何处理连续的动作空间?回归函数拟合
DPG
神经网络直接回归到某一个值
$$ a = \mu(s,\theta) $$# DPG off policy
# policy update net
class ActorNetwork(nn.Module):
def __init__(self, input_dim, output_dim, action_high, action_low):
super().__init__()
self.fc1 = nn.Linear(input_dim, 128)
self.fc2 = nn.Linear(128, 128)
self.actor_fc = nn.Linear(128, output_dim)
# Action scaling parameters.
self.action_high = torch.FloatTensor(action_high)
self.action_low = torch.FloatTensor(action_low)
self.action_range = self.action_high - self.action_low
def forward(self, x):
x1 = torch.relu(self.fc1(x))
x2 = torch.relu(self.fc2(x1))
# Scale to environment's action range
action = torch.tanh(self.actor_fc(x2))
scaled_action = self.action_low + (action + 1.0) * 0.5 * self.action_range
return scaled_action
# policy evaluation net
class CriticNetwork(nn.Module):
def __init__(self, state_dim, action_dim):
super().__init__()
self.fc1 = nn.Linear(state_dim + action_dim, 128)
self.fc2 = nn.Linear(128, 128)
self.critic_fc = nn.Linear(128, 1)
def forward(self, state, action):
x1 = torch.cat([state, action], dim=-1)
x2 = torch.relu(self.fc1(x1))
x3 = torch.relu(self.fc2(x2))
q_value = self.critic_fc(x3)
return q_value
class DPGAgent:
def __init__(self, state_dim, action_dim, action_high, action_low,
learning_rate_actor, learning_rate_critic,
gamma, tau):
self.state_dim = state_dim
self.action_dim = action_dim
self.tau = tau # Soft update parameter
# Initialize networks
self.actor = ActorNetwork(state_dim, action_dim, action_high, action_low)
self.critic = CriticNetwork(state_dim, action_dim)
# Initialize target networks
self.actor_target = ActorNetwork(state_dim, action_dim, action_high, action_low)
self.critic_target = CriticNetwork(state_dim, action_dim)
# Copy weights to target networks
self.hard_update(self.actor_target, self.actor)
self.hard_update(self.critic_target, self.critic)
# Optimizers
self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=learning_rate_actor)
self.critic_optimizer = optim.Adam(self.critic.parameters(), lr=learning_rate_critic)
# Experience replay buffer
self.batch_size = 64
self.memory_size = 10000
self.memory = deque(maxlen=self.memory_size)
self.learning_step = 0
self.target_update_freq = 100
# For exploration
self.noise_std = 0.1
self.noise_decay = 0.999
def hard_update(self, target, source):
"""Copy weights from source to target network"""
for target_param, param in zip(target.parameters(), source.parameters()):
target_param.data.copy_(param.data)
def soft_update(self, target, source):
"""Soft update target network parameters"""
for target_param, param in zip(target.parameters(), source.parameters()):
target_param.data.copy_(self.tau * param.data + (1.0 - self.tau) * target_param.data)
def get_action(self, state, training=True):
state_tensor = torch.FloatTensor(state).unsqueeze(0)
action = self.actor(state_tensor).detach().numpy()[0]
if training:
# Add exploration noise
noise = np.random.normal(0, self.noise_std, size=self.action_dim)
action = np.clip(action + noise, self.actor.action_low.numpy(), self.actor.action_high.numpy())
return action
def store_experience(self, state, action, reward, next_state, done):
self.memory.append((state, action, reward, next_state, done))
def update_policy(self):
if len(self.memory) < self.batch_size:
return 0, 0
# Sample batch from replay buffer
batch = random.sample(self.memory, self.batch_size)
states, actions, rewards, next_states, dones = zip(*batch)
states = torch.FloatTensor(states)
actions = torch.FloatTensor(actions)
rewards = torch.FloatTensor(rewards).unsqueeze(1)
next_states = torch.FloatTensor(next_states)
dones = torch.BoolTensor(dones).unsqueeze(1)
# Update Critic
with torch.no_grad():
next_actions = self.actor_target(next_states)
target_q = self.critic_target(next_states, next_actions)
target = rewards + gamma * target_q * (~dones).float()
current_q = self.critic(states, actions)
critic_loss = nn.MSELoss()(current_q, target)
self.critic_optimizer.zero_grad()
critic_loss.backward()
torch.nn.utils.clip_grad_norm_(self.critic.parameters(), max_norm=0.5)
self.critic_optimizer.step()
# Update Actor
policy_actions = self.actor(states)
actor_loss = -self.critic(states, policy_actions).mean()
self.actor_optimizer.zero_grad()
actor_loss.backward()
torch.nn.utils.clip_grad_norm_(self.actor.parameters(), max_norm=0.5)
self.actor_optimizer.step()
# Soft update target networks
self.soft_update(self.actor_target, self.actor)
self.soft_update(self.critic_target, self.critic)
self.learning_step += 1
# Hard update target networks
if self.learning_step % self.target_update_freq == 0:
self.hard_update(self.actor_target, self.actor)
self.hard_update(self.critic_target, self.critic)
# Decay exploration noise
self.noise_std *= self.noise_decay
return actor_loss.item(), critic_loss.item()
def get_policy(self, states):
"""Extract deterministic policy"""
policy = []
with torch.no_grad():
for state in states:
state_tensor = torch.FloatTensor(state).unsqueeze(0)
action = self.actor(state_tensor).numpy()[0]
policy.append(action)
return np.array(policy)
def train_dpg(env, n_episodes=1000):
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
action_high = env.action_space.high
action_low = env.action_space.low
agent = DPGAgent(state_dim, action_dim, action_high, action_low)
for episode in range(n_episodes):
total_reward = 0
state = env.reset()
done = False
step_count = 0
while not done:
action = agent.get_action(state)
next_state, reward, done, truncated, _ = env.step(action)
total_reward += reward
done = done or truncated
agent.store_experience(state, action, reward, next_state, done)
actor_loss, critic_loss = agent.update_policy()
state = next_state
step_count += 1
if episode % 100 == 0:
print(f"Episode {episode}, Total Reward: {total_reward:.2f}, Steps: {step_count}")
print(f" Actor Loss: {actor_loss:.4f}, Critic Loss: {critic_loss:.4f}")
print(f" Noise STD: {agent.noise_std:.4f}")
return agent
def test_dpg(env, agent):
state = env.reset()
done = False
total_reward = 0
while not done:
action = agent.get_action(state, training=False) # No exploration during test
next_state, reward, done, truncated, _ = env.step(action)
done = done or truncated
total_reward += reward
state = next_state
print(f"Test Reward: {total_reward}")